Question

函数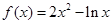在其定义域的一个子区间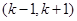内部是单调函数，则实数 的取值范围是 （    ）

A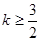．	B．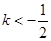
C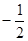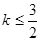．＜	D．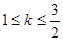

Answer 1

A

解析试题分析：求导函数，f′(x)=4x-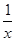，当k=1时，（k-1，k+1）为（0，2），函数在(0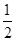，)上单调减，在(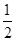，2)上单调增，满足题意；当k≠1时，∵函数f（x）=2x²-lnx在其定义域的一个子区间（k-1，k+1）内不是单调函数
∴f′（x）在其定义域的一个子区间（k-1，k+1）内有正也有负
∴f′（k-1）f′（k+1）＜0
∴(4k-4-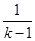)(4k+4-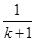)＜0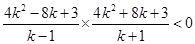
∴
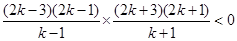
∵k-1＞0∴k+1＞0，，2k+1＞0，2k+3＞0，
∴（2k-3）（2k-1）＞＜0，解得1＜k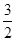＜综上知，1≤k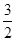＜，故可知如果内部有单调性，则可知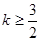，故选A．
考点：本题主要是考查以函数为载体，考查函数的单调性，考查学生分析解决问题的能力.
点评：解决该试题的关键是分类讨论，等价转化．利用反面的结论先期间诶内部不是单调函数，进而得到内部是单调函数的参数范围，