
【题目】已知函数f(x)=2x , x∈(0,2)的值域为A,函数g(x)=log2(x﹣2a)+ ![]() (a<1)的定义域为B.
(a<1)的定义域为B.
(Ⅰ)求集合A,B;
(Ⅱ)若BA,求实数a的取值范围.
【答案】解:(Ⅰ)已知函数f(x)=2x , x∈(0,2)的值域为A,∴A=(1,4),
函数g(x)=log2(x﹣2a)+ ![]() (a<1)的定义域为B.
(a<1)的定义域为B.
∴B=(2a,a+1),a<1,
(Ⅱ)若BA,则(2a,a+1)(1,4),
∴ 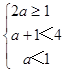 ,解得:
,解得: ![]() ≤a<1
≤a<1
【解析】(Ⅰ)根据指数函数以及对数函数的性质解出即可;(2)根据集合的包含关系得到关于a的不等式组,解出即可.
【考点精析】掌握集合的表示方法-特定字母法和函数的定义域及其求法是解答本题的根本,需要知道①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合;求函数的定义域时,一般遵循以下原则:①
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合;求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】下列命题:
①函数y=﹣ ![]() 在其定义域上是增函数;
在其定义域上是增函数;
②函数y= ![]() 是奇函数;
是奇函数;
③函数y=log2(x﹣1)的图象可由y=log2(x+1)的图象向右平移2个单位得到;
④若( ![]() )a=(
)a=( ![]() )b<1.则a<b<0
)b<1.则a<b<0
则下列正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣log3(9x)log3 ![]() (
( ![]() ≤x≤27).
≤x≤27).
(1)设t=log3x,求t的取值范围
(2)求f(x)的最小值,并指出f(x)取得最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2+mx+1=0有两个不等的负实数根;命题q:方程4x2+4(m﹣2)x+1=0无实数根.
(1)若“¬p”为假命题,求m范围;
(2)若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
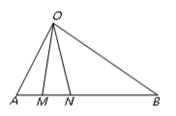
【题目】如图所示,某公路![]() 一侧有一块空地
一侧有一块空地![]() ,其中
,其中 ![]() ,
,![]() .当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
(1)若M在距离A点2 km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
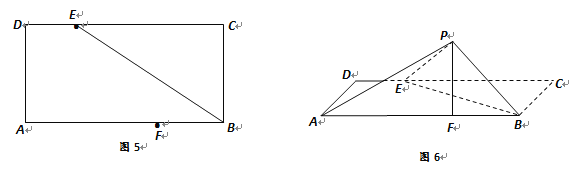
【题目】如图![]() ,矩形
,矩形![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() 边上的点,且
边上的点,且![]() ,将
,将![]() 沿
沿![]() 折起至
折起至![]() 位置(如图
位置(如图![]() 所示),连结
所示),连结![]() ,其中
,其中![]() .
.
(Ⅰ) 求证: ![]() ;
;
(Ⅱ) 在线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(Ⅲ) 求点![]() 到
到![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com