[题目]已知F1.F2分别是双曲线 ﹣ =1的左.右焦点.过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M.若点M在以线段F1F2为直径的圆外.则双曲线离心率的取值范围是( )A.(1. )B.( .+∞)C.( .2)D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知F1、F2分别是双曲线 ﹣ =1（a＞0，b＞0）的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆外，则双曲线离心率的取值范围是（）
A.（1，）
B.（，+∞）
C.（，2）
D.（2，+∞）

【答案】D
【解析】解：双曲线 ﹣ =1的渐近线方程为y=± x，

不妨设过点F2与双曲线的一条渐过线平行的直线方程为y= （x﹣c），

与y=﹣ x联立，可得交点M（，﹣ ），

∵点M在以线段F1F2为直径的圆外，

∴|OM|＞|OF2|，即有＞c2，

∴b2＞3a2，

∴c2﹣a2＞3a2，即c＞2a．

则e= ＞2．

∴双曲线离心率的取值范围是（2，+∞）．

故选：D．

根据斜率与平行的关系即可得出过焦点F2的直线，与另一条渐近线联立即可得到交点M的坐标，再利用点M在以线段F1F2为直径的圆外和离心率的计算公式即可得出．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】2011年，国际数学协会正式宣布，将每年的3月14日设为国际数学节，来源则是中国古代数学家祖冲之的圆周率．祖冲之，在世界数学史上第一次将圆周率（π）值计算到小数点后的第7位，即3.1415926到3.1415927之间，数列{an}是公差大于0的等差数列，其前三项是“31415926”中连续的三个数，数列{bn}是等比数列，其公比大于1的正整数且前三项是“31415926”中的三个数，且a3=b3 ．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）cn= 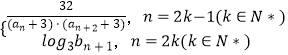，求c1+c2+c3+…+c ．（n∈N*）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在某次试验中,有两个试验数据，统计的结果如下面的表格1.

（1）在给出的坐标系中画出的散点图; 并判断正负相关；

（2）填写表格2,然后根据表格2的内容和公式求出对的回归直线方程，并估计当为10时的值是多少？（公式：，）

	1	2	3	4	5
	2	3	4	4	5

表1

表格2

序号
1	1	2
2	2	3
3	3	4
4	4	4
5	5	5

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在极坐标系中，曲线C：ρ=2acosθ（a＞0），l：ρcos（θ﹣ ）= ，C与l有且仅有一个公共点．
（Ⅰ）求a；
（Ⅱ）O为极点，A，B为C上的两点，且∠AOB= ，求|OA|+|OB|的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= ，若存在实数x1 ， x2 ， x3 ， x4满足f（x1）=f（x2）=f（x3）=f（x4），其中x1＜x2＜x3＜x4 ，则x1x2x3x4取值范围是（）
A.（60，96）
B.（45，72）
C.（30，48）
D.（15，24）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥S﹣ABCD中，底面ABCD为直角梯形，AB∥CD，BC⊥CD，平面SCD⊥平面ABCD，SC=SD=CD=AD=2AB，M，N分别为SA，SB的中点，E为CD中点，过M，N作平面MNPQ分别与BC，AD交于点P，Q，若 =t ．
（1）当t= 时，求证：平面SAE⊥平面MNPQ；
（2）是否存在实数t，使得二面角M﹣PQ﹣A的平面角的余弦值为？若存在，求出实数t的值；若不存在，说明理由．