
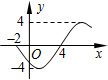
 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$). 分析 根据三角函数的图象确定A,ω和φ的值即可得到结论.
解答 解:由图象知A=4,T=2[4-(-2)]=12,
则T=$\frac{2π}{ω}$=12,即ω=$\frac{π}{6}$,
则f(x)=4sin($\frac{π}{6}$x+φ),
由五点对应法得$\frac{π}{6}$×4+φ=0,
即φ=-$\frac{2π}{3}$,
故f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$),
故答案为:f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
点评 本题主要考查三角函数解析式的求解,根据三角函数图象确定A,ω和φ的值是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=tanx | B. | y=|sinx| | C. | y=sin2x | D. | y=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
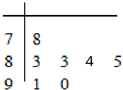 在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
在“南安一中校园歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85和6.8 | B. | 85和1.6 | C. | 86和6.8 | D. | 86和1.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com