
【题目】(本小题满分12分)已知椭圆![]() :
:![]() 与抛物线
与抛物线![]() :
:![]() 有相同焦点
有相同焦点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知直线![]() 过椭圆
过椭圆![]() 的另一焦点
的另一焦点![]() ,且与抛物线
,且与抛物线![]() 相切于第一象限的点
相切于第一象限的点![]() ,设平行
,设平行![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当△
两点,当△![]() 面积最大时,求直线
面积最大时,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)由于抛物线![]() 的焦点为
的焦点为![]() ,得到
,得到![]() ,又
,又![]() 得到
得到![]() .
.
(Ⅱ)思路一:设![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() 直线
直线![]() 的方程为
的方程为![]() 即
即![]() 且过点
且过点![]()
![]() ,
,![]()
![]() 切线
切线![]() 方程为
方程为![]()
由![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立方程组
,联立方程组
由 ,消
,消![]() 整理得
整理得![]()
![]()
设![]() ,
,![]() ,应用韦达定理
,应用韦达定理 ![]()
得![]()
![]() ,由点
,由点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]()
![]() 应用基本不等式等号成立的条件求得
应用基本不等式等号成立的条件求得![]()
思路二:![]() ,由已知可知直线
,由已知可知直线![]() 的斜率必存在,设直线
的斜率必存在,设直线![]()
由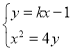 消去
消去![]() 并化简得
并化简得![]()
根据直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() .得到
.得到![]() ,
,![]() .
.
根据切点![]() 在第一象限得
在第一象限得![]() ;由
;由![]() ∥
∥![]() ,设直线
,设直线![]() 的方程为
的方程为![]()
由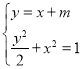 ,消去
,消去![]() 整理得
整理得![]() , 思路同上.
, 思路同上.
试题解析:(Ⅰ)![]() 抛物线
抛物线![]() 的焦点为
的焦点为![]() ,
,
![]() ,又
,又![]()
![]() 椭圆方程为
椭圆方程为![]() . 4分
. 4分
(Ⅱ)(法一)设![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() 直线
直线![]() 的方程为
的方程为![]() 即
即![]() 且过点
且过点![]()
![]() ,
,![]()
![]() 切线
切线![]() 方程为
方程为![]() 6分
6分
因为![]() ,所以设直线
,所以设直线![]() 的方程为
的方程为![]() ,
,
由 ,消
,消![]() 整理得
整理得![]() 7分
7分
![]() ,解得
,解得![]() ①
①
设![]() ,
,![]() ,则
,则
![]()
∴![]()
![]() 8分
8分
直线![]() 的方程为
的方程为![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]() 9分
9分
![]()
![]() , 10分
, 10分
由①![]() ,
, ![]()
![]() (当且仅当
(当且仅当![]() 即
即![]() 时,取等号)
时,取等号)
![]() 最大
最大![]()
所以,所求直线![]() 的方程为:
的方程为:![]() . 12分
. 12分

(法二)![]() ,由已知可知直线
,由已知可知直线![]() 的斜率必存在,
的斜率必存在,
设直线![]()
由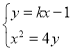 消去
消去![]() 并化简得
并化简得![]()
∵直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() .
.
∴![]() ,得
,得![]() . 5分
. 5分
∵切点![]() 在第一象限.
在第一象限.
∴![]() 6分
6分
∵![]() ∥
∥![]()
∴设直线![]() 的方程为
的方程为![]()
由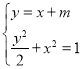 ,消去
,消去![]() 整理得
整理得![]() , 7分
, 7分
![]() ,解得
,解得![]() .
.
设![]() ,
,![]() ,则
,则
![]() ,
,![]()
![]() . 8分
. 8分
又直线![]() 交
交![]() 轴于
轴于![]()
![]() 10分
10分
![]()
当![]() ,即
,即![]() 时,
时,![]() . 11分
. 11分
所以,所求直线![]() 的方程为
的方程为![]() . 12分
. 12分


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
男性用户:
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6.635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求2名用户中评分小于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附: 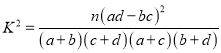
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市某水产养殖户进行小龙虾销售,已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系为:
(天)之间的函数关系为:
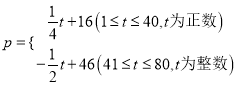 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
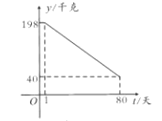
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠![]() 元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间
元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com