练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在三棱锥A－BCD中，侧棱AB、AC、AD两两垂直，△ ABC、△ACD、△ADB的面积分别为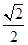,,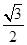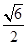则三棱锥A－BCD的外接球的体积为______________．

     

    【答案】

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （06年江西卷理）（12分）

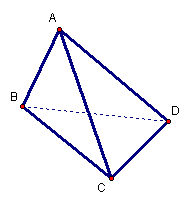
    如图，在三棱锥A－BCD中，侧面ABD、ACD

    是全等的直角三角形，AD是公共的斜边，

    且AD＝，BD＝CD＝1，另一个侧面是正三角形

    （1）求证：AD^BC

    （2）求二面角B－AC－D的大小

    （3）在直线AC上是否存在一点E，使ED与面BCD

    成30°角？若存在，确定E的位置；若不存在，说明理由。

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年四川省绵阳市高三12月月考理科数学试卷（解析版） 题型：选择题

    如图所示，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下列命题正确的是(　　)

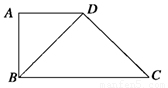
    A. 平面ABD⊥平面ABC             B. 平面ADC⊥平面BDC

    C. 平面ABC⊥平面BDC             D. 平面ADC⊥平面ABC

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学空间图形的基本关系与公理、空间图形的平行关系专项训练（河北） 题型：解答题

    如右图所示，在三棱锥A－BCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．

    (1)求证：四边形EFGH是平行四边形；

    (2)若AC＝BD，求证：四边形EFGH是菱形；

    (3)当AC与BD满足什么条件时，四边形EFGH是正方形

     

    查看答案和解析>>

    科目：高中数学 来源：2014届河北省高一上学期二调数学 题型：选择题

    如图，四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB沿BD折起，

    使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下列命题正确的是(　　)

    A．平面ADC⊥平面ABC

    B．平面ADC⊥平面BDC

    C．平面ABC⊥平面BDC

    D．平面ABD⊥平面ABC

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案