
已知椭圆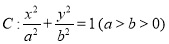 的离心率为
的离心率为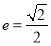 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线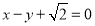 相切.
相切.
(1)求椭圆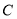 的标准方程;
的标准方程;
(2)过右焦点 作斜率为
作斜率为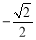 的直线
的直线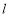 交曲线
交曲线 于
于 、
、 两点,且
两点,且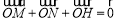 ,又点
,又点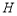 关于原点
关于原点 的对称点为点
的对称点为点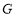 ,试问
,试问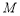 、
、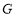 、
、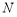 、
、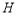 四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(1)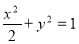 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)设出圆的方程,利用圆心到直线的距离等于半径,求出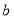 ,利用离心率及
,利用离心率及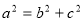 ,求出
,求出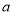 ,即可求出椭圆
,即可求出椭圆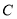 的标准方程;
的标准方程;
(2)求出直线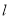 的方程,联立直线方程与椭圆方程,设
的方程,联立直线方程与椭圆方程,设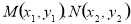 ,利用
,利用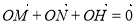
,求出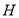 坐标,又点
坐标,又点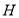 关于原点
关于原点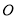 的对称点为点
的对称点为点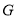 求出
求出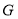 的坐标,推出线段
的坐标,推出线段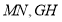 的中垂线方程
的中垂线方程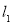 和
和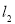 ,然后求出
,然后求出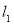 和
和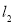 的交点为
的交点为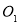 ,推出
,推出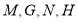 四点共圆.
四点共圆.
试题解析:(1)由题意可得圆的方程为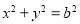 ,
,
∵直线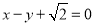 与圆相切,∴
与圆相切,∴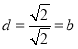 ,即
,即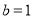 , 2分
, 2分
又 ,及
,及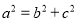 ,得
,得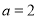 ,所以椭圆方程为
,所以椭圆方程为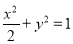 . 4分
. 4分
(2)因直线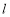 过点
过点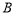 ,且斜率为
,且斜率为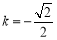 ,故有
,故有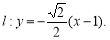
联立方程组 ,消去
,消去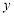 ,得
,得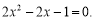 6分
6分
设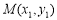 、
、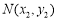 ,可得
,可得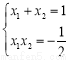 ,于是
,于是 .
.
又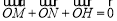 ,得
,得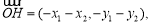 即
即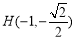 8分
8分
而点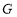 与点
与点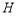 关于原点对称,于是,可得点
关于原点对称,于是,可得点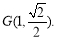
若线段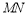 、
、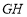 的中垂线分别为
的中垂线分别为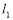 和
和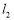 ,
,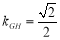 ,则有
,则有
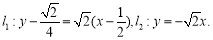
联立方程组 ,解得
,解得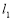 和
和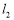 的交点为
的交点为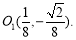 10分
10分
因此,可算得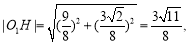
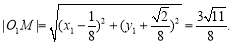
所以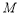 、
、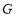 、
、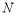 、
、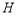 四点共圆,且圆心坐标为
四点共圆,且圆心坐标为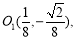 半径为
半径为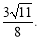 12分
12分
考点:直线与圆锥曲线的综合性问题


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试文科数学试卷(解析版) 题型:解答题
过抛物线C: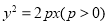 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,且直线AB过点(0,-1),求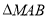 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试文科数学试卷(解析版) 题型:选择题
程序框图如图所示:
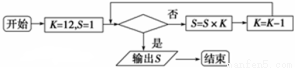
如果上述程序运行的结果S=1320,那么判断框中应填入( )
A.K<10! B.K≤10! C.K<9? ! D.K≤11!
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试文科数学试卷(解析版) 题型:选择题
已知复数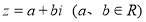 ,
,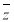 是
是 的共轭复数,且
的共轭复数,且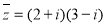 则a、b的值分别为( )
则a、b的值分别为( )
A. 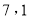 B.
B.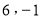 C.
C.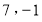 D.
D.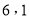
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三年级模拟考试理科数学试卷(解析版) 题型:选择题
抛物线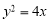 的焦点为
的焦点为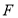 ,点
,点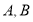 在抛物线上,且
在抛物线上,且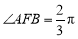 ,弦
,弦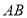 中点
中点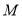 在准线
在准线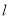 上的射影为
上的射影为 的最大值为( )
的最大值为( )
A.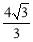 B.
B.
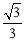 C.
C.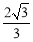 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷(解析版) 题型:解答题
近年来,我国很多城市都出现了严重的雾霾天气.为了更好地保护环境,2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:
组别 | PM2.5浓度(微克/立方米) | 频数(天) |
第一组 | (0,35] | 24 |
第二组 | (35,75] | 48 |
第三组 | (75,115] | 12 |
第四组 | >115 | 6 |
(1)在这 天中抽取
天中抽取 天的数据做进一步分析,每一组应抽取多少天?
天的数据做进一步分析,每一组应抽取多少天?
(2)在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com