
 )sin2x+
)sin2x+ sin(x+
sin(x+ )sin(x-
)sin(x- ).
). =0时,求f(x)在区间[
=0时,求f(x)在区间[ ,
, ]上的取值范围;
]上的取值范围; =2时,f(
=2时,f( )=
)= ,求
,求 的值.
的值. ];(2)-2.
];(2)-2. (sin2x-cos2x)+
(sin2x-cos2x)+
 sin(2x-
sin(2x- )+
)+ ,……………………(3分)
,……………………(3分) ,
, ]得2x-
]得2x- ∈[0,
∈[0, ],所以sin(2x-
],所以sin(2x- )∈[-
)∈[- ,1],
,1], sin(2x-
sin(2x- )+
)+ ∈[0,
∈[0, ].……………………(6分)
].……………………(6分) cos2x=
cos2x=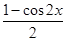 +
+ sin2x-
sin2x- cos2x
cos2x [sin2x-(1+m)cos2x]+
[sin2x-(1+m)cos2x]+ ,………………………………(8分)
,………………………………(8分) =
= =
= ,
, =
= =-
=- ,……………………(10分)
,……………………(10分) =
= [
[ +(1+m)
+(1+m) ]+
]+ ,得m=-2.………………(12分)
,得m=-2.………………(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com