
设函数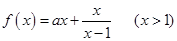
(1)若a>0,求函数 的最小值;
的最小值;
(2)若a是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数,求f (x)>b恒成立的概率。
(1) 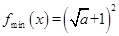 (2)
(2) 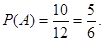
【解析】
试题分析: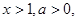
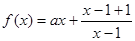
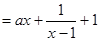
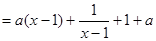
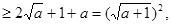
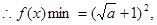
于是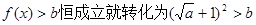 成立。
成立。
设事件A:“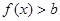 恒成立”,则
恒成立”,则
基本事件总数为12个,即
(1,2),(1,3),(1,4),(1,5);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5);
事件A包含事件:(1,2),(1,3);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5)共10个
由古典概型得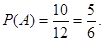
考点:基本不等式;古典概型。
点评:本题考查用列举法计算基本事件数及随机事件发生的概率,解题的关键是熟练运用分类列举的方法及事件的性质将所有的基本事件一一列举出来,运用公式求出概率,注意列举时要不重不漏。列举法求概率适合基本事件数不太多的概率求解问题。


科目:高中数学 来源: 题型:
(08年滨州市质检三理) 设函数![]() .
.
(1)若![]() 过两点(0,0)、(a,0)的中点作与x轴垂直的直线,此直线与函数
过两点(0,0)、(a,0)的中点作与x轴垂直的直线,此直线与函数![]() 的图象交于点
的图象交于点![]() ,求证函数
,求证函数![]() 的点p处的切点过点(b,0);
的点p处的切点过点(b,0);
(2)若![]() ,且当
,且当![]() 时
时![]() 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省高三高考适应性测试理科数学试卷(解析版) 题型:解答题
设函数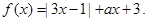
(1)若a=1,解不等式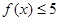 ;
;
(2)若函数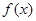 有最小值,求实数a的取值范围。
有最小值,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010年陕西省高二第一学期期中考试数学卷 题型:解答题
(理科做) 设函数
(1)若a>0,求函数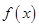 的最小值;
的最小值;
(2)若a是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数,
求f (x)>b恒成立的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
(理科做) 设函数![]()
(1)若a>0,求函数![]() 的最小值;
的最小值;
(2)若a是从1,2,3三个数中任取一个数,b是从2,3,4,5四个数中任取一个数,求f (x)>b恒成立的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com