
分析 (1)根据指数幂的运算性质即可求出.
(2)根据对数的运算法则和对数的换底公式进行化简即可.
解答 解:(1)显然x>0,令$a=2{x^{\frac{1}{2}}},b={x^{-\frac{1}{2}}}$,则已知a2+b2=6,ab=2,
∴${(a+b)^2}={a^2}+{b^2}+2ab=10,a+b=\sqrt{10}$,
∴$8{x^{\frac{3}{2}}}+{x^{-\frac{3}{2}}}={a^3}+{b^3}=(a+b)({a^2}-ab+{b^2})=4\sqrt{10}$,
(2)∵$\left\{{\begin{array}{l}{{{log}_3}2=\frac{lg2}{lg3}=m}\\{{{log}_5}3=\frac{lg3}{lg5}=\frac{lg3}{1-lg2}=n}\end{array}}\right.∴\left\{{\begin{array}{l}{lg2=\frac{mn}{mn+1}}\\{lg3=\frac{n}{mn+1}}\end{array}}\right.$,
∴${log_4}15=\frac{lg15}{lg4}=\frac{lg3+lg5}{2lg2}=\frac{lg3-lg2+1}{2lg2}=\frac{n+1}{2mn}$.
点评 本题主要指数查对数的化简,根据对数的换底公式以及对数的运算法则是解决本题的关键


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4+3\sqrt{3}}}{10}$ | B. | $\frac{{4-3\sqrt{3}}}{10}$ | C. | $\frac{{3\sqrt{3}-4}}{10}$ | D. | $\frac{{-3\sqrt{3}-4}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有1个白球,至多有1个白球 | B. | 至少有1个白球,至少有1个红球 | ||
| C. | 至少有1个白球,没有白球 | D. | 至少有1个白球,红、黑球各1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
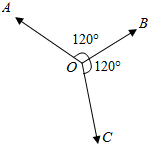
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=1,b=2,c=3 | B. | b=c=1,∠B=45° | C. | a=1,b=2,∠A=100° | D. | a=1,b=$\sqrt{2},∠A={30°}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com