在中.两直角边分别为..设为斜边上的高.则.由此类比:三棱锥中的三条侧棱..两两垂直.且长度分别为...设棱锥底面上的高为.则．题目和参考答案——青夏教育精英家教网—

在中，两直角边分别为、，设为斜边上的高，则，由此类比：三棱锥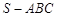中的三条侧棱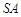、、两两垂直，且长度分别为、、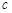，设棱锥底面上的高为，则　　　　　　　　　　　　．

解析试题分析：立体几何中的类比推理主要是基本元素之间的类比：平面?空间，点?点或直线，直线?直线或平面，平面图形?平面图形或立体图形，故本题由平面上的直角三角形中的边与高的关系式类比立体中两两垂直的棱的三棱锥中边与高的关系即可．解：∵PA、PB、PC两两互相垂直，∴PA⊥平面PBC．由已知有,所以，故可知答案为。
考点：类比推理
点评: 类比推理是指依据两类数学对象的相似性，将已知的一类数学对象的性质类比迁移到另一类数学对象上去．其思维过程大致是：观察、比较联想、类推猜测新的结论

练习册系列答案

赢在起跑线快乐暑假河北少年儿童出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

古希腊著名的毕达哥拉斯学派把1、3、6、10 这样的数称为“三角形数”，而把1、4、9、16 这样的数称为“正方形数”.如图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式中，符合这一规律的表达式是　　
①13=3+10； ②25=9+16 ③36=15+21； ④49=18+31；⑤64=28+36

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

在平面几何里，有勾股定理：“设的两边AB、AC互相垂直，则。”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得到的正确结论是：“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直，则 ”

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

平面上有条直线, 这条直线任意两条不平行, 任意三条不共点, 记这条直线将平面分成部分, 则___________, 时,_________________.)(用表示).

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

已知：；
通过观察上述两等式的规律，请你写出一般性的命题：___________________.

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

若数轴上不同的两点分别与实数对应，则线段的中点与实数对应，由此结论类比到平面得，若平面上不共线的三点分别与二元实数对对应，则的重心与对应.

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

设n为正整数，f(n)＝1＋＋＋…＋，计算得f(2)＝，f(4)>2，f(8)>，f(16)>3，观察上述结果，可推测一般的结论为_______________________________．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

专家由圆x+y=a的面积S=a通过类比推理猜想椭圆的面积S=ab. 之后利用演绎推理证明了这个公式是对的! 在平面直角坐标系中, 点集A="{" (x, y)| }, 点集B="{(x," y)| 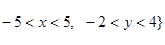, 则点集M="{(x," y)|x=x+x, y=y+y, (x, y)A, (x, y)B}所表示的区域的面积为_____________.