【题目】若椭圆的对称轴为坐标轴，长轴长与短轴长的和为18，焦距为6，则椭圆的方程为（ ）
A.
B.
C. 或 
D.以上都不对
【答案】C
【解析】解：设椭圆的长半轴与短半轴分别为a和b，
则2（a+b）=18，即a+b=9①，
由焦距为6，得到c=3，则a2﹣b2=c2=9②，
由①得到a=9﹣b③，把③代入②得：
（9﹣b）2﹣b2=9，化简得：81﹣18b=9，解得b=4，把b=4代入①，解得a=5，
所以椭圆的方程为： 
或 
．
故选C．
设出椭圆的长半轴与短半轴分别为a和b，根据长轴与短轴的和为18列出关于a与b的方程记作①，由焦距等于6求出c的值，根据椭圆的基本性质a2﹣b2=c2 ， 把c的值代入即可得到关于a与b的另一关系式记作②，将①②联立即可求出a和b的值，然后利用a与b的值写出椭圆的方程即可．
阅读快车系列答案科目：高中数学 来源： 题型：
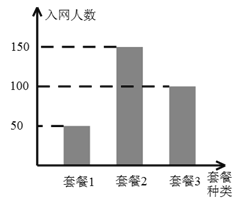
【题目】移动公司在春节正月初八这天推出4G套餐，对这天办理套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元. 初八当天参与活动的人数统计结果如图所示，
（Ⅰ）从参加当天活动的人中任选一人，求此人获得优惠金额不低于300元的概率（将频率视为概率）；
（Ⅱ）若采用分层抽样的方式从参加活动的客户中选出6人，再从该6人中随机选两人，求这两人获得相等优惠金额的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某生产甲，乙两种产品，生产这两种产品每吨需要的煤，电以及每吨产品的产值如表所示．若每天配给该厂的煤至多56吨，供电至多45千瓦，问该厂如何安排生产，使该厂日产值最大？
用煤/吨 | 用电/千瓦 | 产值/万元 | |
甲种产品 | 7 | 2 | 8 |
乙种产品 | 3 | 5 | 11 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递减，若f（log2a）+f（2log 
a）≥2f（﹣1），则实数a的取值范围是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=2x+2﹣x ．
（1）用定义法证明：函数f（x）是区间（0，+∞）上的增函数；
（2）若x∈[﹣1，2]，求函数g（x）=2x[f（x）﹣2]﹣3的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足 
， 
，n∈N* ．
（1）求证：数列 
为等比数列；
（2）是否存在互不相等的正整数m，s，t，使m，s，t成等差数列，且am﹣1，as﹣1，at﹣1成等比数列？如果存在，求出所有符合条件的m，s，t；如果不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
