
【题目】已知圆M过两点A(1,﹣1),B(﹣1,1),且圆心M在直线x+y﹣2=0上.
(1)求圆M的方程.
(2)设P是直线3x+4y+8=0上的动点,PC、PD是圆M的两条切线,C、D为切点,求四边形PCMD面积的最小值.
【答案】
(1)解:设圆心M(a,b),则a+b﹣2=0①,
又A(1,﹣1),B(﹣1,1),
∴kAB= ![]() =﹣1,
=﹣1,
∴AB的垂直平分线l的斜率k=1,又AB的中点为O(0,0),
∴l的方程为y=x,而直线l与直线x+y﹣2=0的交点就是圆心M(a,b),
由 ![]() 解得:
解得: ![]() ,又r=|MA|=2,
,又r=|MA|=2,
∴圆M的方程为(x﹣1)2+(y﹣1)2=4.
(2)解:如图:

SPCMD=|MC||PC|=2 ![]() =2
=2 ![]() ,
,
又点M(1,1)到3x+4y+8=0的距离d=|MN|= ![]() =3,
=3,
所以|PM|min=d=3,
所以(SPCMD)min=2 ![]() =2
=2 ![]() .
.
【解析】(1)设圆心M(a,b),依题意,可求得AB的垂直平分线l的方程,利用方程组可求得直线l与直线x+y﹣2=0的交点,即圆心M(a,b),再求得r=|MA|=2,即可求得
圆M的方程;(2)作出图形,易得SPCMD=|MC||PC|=2 ![]() =2
=2 ![]() ,利用点到直线间的距离公式可求得|PM|min=d=3,从而可得(SPCMD)min=2
,利用点到直线间的距离公式可求得|PM|min=d=3,从而可得(SPCMD)min=2 ![]() .
.


科目:高中数学 来源: 题型:
【题目】在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?( )
A.9日
B.8日
C.16日
D.12日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() (a>0,b>0)的两条渐近线与抛物线D:y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点,双曲线的离心率为
(a>0,b>0)的两条渐近线与抛物线D:y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点,双曲线的离心率为 ![]() ,△ABO的面积为2
,△ABO的面积为2 ![]() .
.
(1)求双曲线C的渐近线方程;
(2)求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点坐标分别为A(﹣1,1),B(7,﹣1),C(﹣2,5),AB边上的中线所在直线为l.
(1)求直线l的方程;
(2)若点A关于直线l的对称点为D,求△BCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如右图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( ) 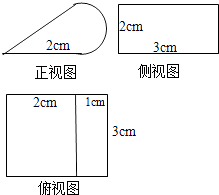
A.19+πcm2
B.22+4πcm2
C.10+6 ![]() +4πcm2
+4πcm2
D.13+6 ![]() +4πcm2
+4πcm2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中有5个大小形状完全相同的小球,其中黑色小球有3个,标号分别为1,2,3,白色小球有2个,标号分别为1,2.
(1)若从盒中任取两个小球,求取出的小球颜色相同且标号之和小于或等于4的概率;
(2)若盒子里再放入一个标号为4的红色小球,从中任取两个小球,求取出的两个小球颜色不同且标号之和大于3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y= ![]() sin(ωx+
sin(ωx+ ![]() )(ω>0).
)(ω>0). 
(1)若ω= ![]() ,求函数的单调增区间和对称中心;
,求函数的单调增区间和对称中心;
(2)函数的图象上有如图所示的A,B,C三点,且满足AB⊥BC. ①求ω的值;
②求函数在x∈[0,2)上的最大值,并求此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD 
(1)求二面角B﹣AD﹣F的大小;
(2)求直线BD与EF所成的角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com