Question

18．已知f（x）对任意x∈[0，+∞），都有f（x+1）=-f（x），当x∈[0，1）时，f（x）=x，若函数g（x）=f（x）-${log}_{{a}^{（x+1）}}$（0＜a＜1）在区间[0，6]上有3个零点，则实数a的取值范围是（　　）

• A． [$\frac{1}{7}$，$\frac{1}{5}$）
• B． （$\frac{1}{7}$，$\frac{1}{5}$）
• C． （0，$\frac{1}{7}$）
• D． （$\frac{1}{5}$，1）

Answer 1

分析 由题意，作出函数y=f（x）在[0，6]的图象，转化函数g（x）=f（x）-${log}_{{a}^{（x+1）}}$（0＜a＜1）的零点为图象的交点，从而求解．

解答 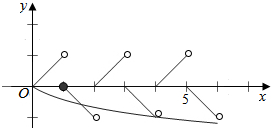解：∵定义在R上的函数y=f（x），
对任意x都有f（x+1）=-f（x），
∴f（x+2）=f[（x+1）=1]=-f（x+1）=f（x），
即函数f（x）是周期为2的周期函数，
若函数g（x）=f（x）-${log}_{{a}^{（x+1）}}$（0＜a＜1）
在区间[0，6]上有3个零点，
则函数y=f（x）与y=log_a（x+1）（0＜a＜1）的图象恰有3个交点，
又由x∈[0，1），f（x）=x，
当x∈[1，2）时，x-1∈[0，1），即有f（x-1）=x-1=-f（x），
即为f（x）=1-x．
在同一坐标系可作出函数y=f（x）
与y=log_a（x+1）（0＜a＜1）在[0，6]的图象如右：
由图可知：函数y=f（x）与y=log_a（x+1）（0＜a＜1）的图象有3个交点时，
当y=log_a（x+1）过（4，-1）时，即有log_a5=-1，解得a=$\frac{1}{5}$；
当y=log_a（x+1）过（6，-1）时，即有log_a7=-1，解得a=$\frac{1}{7}$．
由图象可得a的范围是$\frac{1}{7}$≤a＜$\frac{1}{5}$．
故选A．

点评 本题考查函数方程的转化思想，考查函数的周期性的运用，同时考查函数的解析式的求法和对数的运算性质，运用数形结合的思想方法是解题的关键．