
(本题满分15分)
 如图,已知椭圆
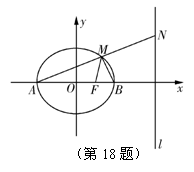
如图,已知椭圆![]() 的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上一动点,且在x轴上方,直线AN与椭圆交于点M.
的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上一动点,且在x轴上方,直线AN与椭圆交于点M.
(1)若AM=MN,求∠AMB的余弦值;
(2)设过A,F,N三点的圆与y轴交于P,Q两点,当
线段PQ的中点坐标为(0,9)时,求这个圆的方程.
(本题满分15分)
解:(1)由已知,![]() ,直线
,直线![]() .
.
设N(8,t)(t>0),因为AM=MN,所以M(4,![]() ).
).
由M在椭圆上,得t=6.故所求的点M的坐标为M(4,3).………………………4分
所以![]() ,
,![]() .
.
![]() .……………………………………7分
.……………………………………7分
(用余弦定理也可求得)
(2)设圆的方程为![]() ,将A,F,N三点坐标代入,得
,将A,F,N三点坐标代入,得

∵ 圆方程为![]() ,令
,令![]() ,得
,得![]() .…11分
.…11分
设![]() ,则
,则 .
.
由线段PQ的中点坐标为(0,9),得![]() ,
,![]() .
.
此时所求圆的方程为![]() .………………………………………15分
.………………………………………15分
(本题用韦达定理也可解)
(2)(法二)由圆过点A、F得圆心横坐标为-1,由圆与y轴交点的纵坐标为(0,9),
得圆心的纵坐标为9,故圆心坐标为(-1,9).…………………………………… 11分
易求得圆的半径为![]() ,………………………………………………………………13分
,………………………………………………………………13分
所以,所求圆的方程为![]() .……………………………………… 15分
.……………………………………… 15分


科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试理科数学 题型:解答题
((本题满分15分)
某有奖销售将商品的售价提高120元后允许顾客有3次抽奖的机会,每次抽奖的方法是在已经设置并打开了程序的电脑上按“Enter”键,电脑将随机产生一个 1~6的整数数作为号码,若该号码是3的倍数则顾客获奖,每次中奖的奖金为100元,运用所学的知识说明这样的活动对商家是否有利。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省招生适应性考试文科数学试卷(解析版) 题型:解答题
(本题满分15分)设函数 .
.
(Ⅰ)若函数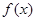 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数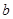 的最大值;
的最大值;
(Ⅱ)若 对任意的
对任意的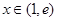 ,
,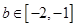 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
注: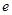 为自然对数的底数.
为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省温州市十校联合体高三上学期期初摸底文科数学 题型:解答题
(本题满分15分)已知直线 与曲线
与曲线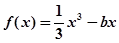 相切
相切
1)求b的值;
2)若方程 在
在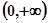 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求
①m的取值范围;
②比较 的大小
的大小
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省温州市十校联合体高三上学期期中考试文科数学 题型:解答题
(本题满分15分)已知抛物线 :
: (
( ),焦点为
),焦点为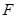 ,直线
,直线 交抛物线
交抛物线 于
于 、
、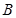 两点,
两点,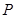 是线段
是线段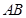 的中点,
的中点,
过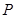 作
作 轴的垂线交抛物线
轴的垂线交抛物线 于点
于点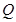 ,
,
(1)若抛物线 上有一点
上有一点 到焦点
到焦点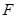 的距离为
的距离为 ,求此时
,求此时 的值;
的值;
(2)是否存在实数 ,使
,使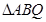 是以
是以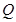 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省六校高三第一次联考文科数学 题型:解答题
(本题满分15分)
已知函数
(1)求 的单调区间;
的单调区间;
(2)设 ,若
,若 在
在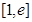 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求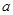 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com