
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若△![]() 的面积为1(
的面积为1(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】在整数集![]() 中,被4除所得余数为
中,被4除所得余数为![]() 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为![]() ,则下列结论正确的为 .
,则下列结论正确的为 .
①2014![]() ;
;
②-1![]() ;
;
③![]() ;
;
④命题“整数![]() 满足
满足![]() ,则
,则![]() ”的原命题与逆命题都正确;
”的原命题与逆命题都正确;
⑤“整数![]() 属于同一类”的充要条件是“
属于同一类”的充要条件是“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 的图像过定点
的图像过定点![]() ;
;
②已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() ,则
,则![]() 的解析式为
的解析式为![]() ;
;
③函数![]() 的图像可由函数
的图像可由函数![]() 图像向右平移一个单位得到;
图像向右平移一个单位得到;
④函数![]() 图像上的点到
图像上的点到![]() 距离的最小值是
距离的最小值是![]() .
.
其中所有正确命题的序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 |
| 0.1 |
第2组 |
| 0.1 |
第3组 |
| 0.4 |
第4组 |
| 0.3 |
第5组 |
| 0.1 |
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
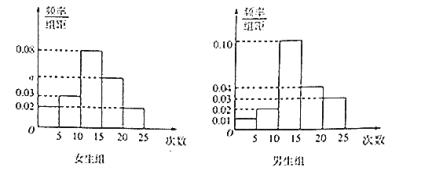
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取3人 ,并用![]() 表示其中男生的人数,求
表示其中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半径为![]() 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰![]() ,其中
,其中![]() 为圆心,
为圆心, ![]() 在圆的直径上,
在圆的直径上, ![]() 在半圆周上,如图.
在半圆周上,如图.
(1)设![]() ,征地面积为
,征地面积为![]() ,求
,求![]() 的表达式,并写出定义域;
的表达式,并写出定义域;
(2)当![]() 满足
满足![]() 取得最大值时,开发效果最佳,求出开发效果最佳的角
取得最大值时,开发效果最佳,求出开发效果最佳的角![]() 的值,
的值,
求出![]() 的最大值.
的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com