Question

某高校组织的自主招生考试，共有1000名同学参加笔试，成绩均介于60分到100分之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分为4组：第1组[60,70），第2组[70,80），第3组[80,90），第4组[90,100].如图是按上述分组方法得到的频率分布直方图，且笔试成绩在85分（含85分）以上的同学有面试资格.

（Ⅰ）估计所有参加笔试的1000名同学中，有面试资格的人数；

（Ⅱ）已知某中学有甲、乙两位同学取得面试资格，且甲的笔试比乙的高；面试时，要求每人回答两个问题，假设甲、乙两人对每一个问题答对的概率均为；若甲答对题的个数不少于乙，则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.

 

Answer 1

【答案】

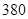（Ⅰ）人；（Ⅱ）.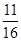

【解析】

试题分析：（Ⅰ）先计算出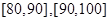内的频率，再计算出满足条件的频率乘以相应的总人数即可；（Ⅱ）应用列举法写出满足条件的所有情况，再找出甲答对题的个数不少于乙的情况数，利用古典概型求解.

试题解析：（Ⅰ）设第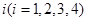组的频率为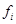，则由频率分布直方图知

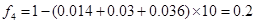        （2分）

所以成绩在85分以上的同学的概率

P≈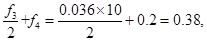             （5分）

故这1000名同学中，取得面试资格的约有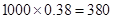人. （6分）

（Ⅱ）设答对记为1，打错记为0，则所有可能的情况有：

甲₀₀乙₀₀，甲₀₀乙₁₀，甲₀₀乙₀₁，甲₀₀乙₁₁，甲₁₀乙₀₀，甲₁₀乙₁₀，甲₁₀乙₀₁，

甲₁₀乙₁₁，甲₀₁乙₀₀，甲₀₁乙₁₀，甲₀₁乙₀₁，甲₀₁乙₁₁，甲₁₁乙₀₀，甲₁₁乙₁₀，

甲₁₁乙₀₁，甲₁₁乙₁₁，共16个               （9分）

甲答对题的个数不少于乙的情况有：

甲₀₀乙₀₀，甲₁₀乙₀₀，甲₁₀乙₁₀，甲₁₀乙₀₁，甲₀₁乙₀₀，甲₀₁乙₁₀，甲₀₁乙₀₁，

甲₁₁乙₀₀，甲₁₁乙₀₁，甲₁₁乙₁₀，甲₁₁乙₁₁，共11个     （11分）

故甲比乙优先获得高考加分资格的概率为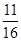.         （12分）

考点：1.频率分布直方图；2.古典概型.