考点:二次函数的性质,函数奇偶性的判断,函数的图象
专题:函数的性质及应用
分析:(1)由已知可得函数的图象是开口朝下,且以y轴为对称轴的抛物线,根据函数解析式,可得函数f(x)=4-x2的图象;
(2)根据函数f(x)的定义域R关于原点对称,且f(-x)=f(x),结合函数奇偶性定义,可得答案.
解答:
(1)解:函数f(x)=4-x
2的图象如下图所示:
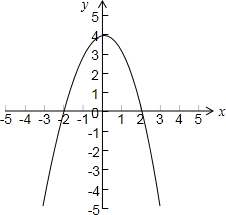
(2)证明:函数f(x)的定义域R关于原点对称,
则f(-x)=4-(-x)
2=4-x
2=f(x),
故函数f(x)为偶函数
点评:本题考查的知识点是二次函数的图象,函数的奇偶性,难度不大,属于基础题.