
【题目】已知抛物线C1:y2=2px(p>0)与双曲线C2: ![]() =1(a>0.b>0)有公共焦点F,且在第一象限的交点为P(3,2
=1(a>0.b>0)有公共焦点F,且在第一象限的交点为P(3,2 ![]() ).
).
(1)求抛物线C1 , 双曲线C2的方程;
(2)过点F且互相垂直的两动直线被抛物线C1截得的弦分别为AB,CD,弦AB、CD的中点分别为G、H,探究直线GH是否过定点,若GH过定点,求出定点坐标;若直线GH不过定点,说明理由.
【答案】
(1)解:P(3,2 ![]() )代入抛物线C1:y2=2px(p>0),可得p=4,∴抛物线C1:y2=8x;
)代入抛物线C1:y2=2px(p>0),可得p=4,∴抛物线C1:y2=8x;
焦点F(2,0),则 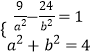 ,∴a=1,b=
,∴a=1,b= ![]() ,∴双曲线C2的方程
,∴双曲线C2的方程 ![]() =1
=1
(2)解:设点A(x1,y1),B(x2,y2),G(x3,y3),H(x4,y4)
把直线AB:y=k(x﹣2)代入y2=8x,得:
k2x2﹣(4k2+8)x+4k2=0,∴x3=2+ ![]() ,y3=k(x3﹣2)=
,y3=k(x3﹣2)= ![]() ,
,
同理可得,x4=2+4k2,y4=﹣4k,
∴kGH= ![]() ,
,
∴直线GH为y﹣ ![]() =
= ![]() (x﹣2﹣
(x﹣2﹣ ![]() ),即y=
),即y= ![]() (x﹣3),过定点P(3,0)
(x﹣3),过定点P(3,0)
【解析】(1)P(3,2 ![]() )代入抛物线C1:y2=2px(p>0),可得p,求出抛物线方程.焦点F(2,0),则
)代入抛物线C1:y2=2px(p>0),可得p,求出抛物线方程.焦点F(2,0),则 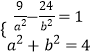 ,求出a,b,可得双曲线C2的方程;(2)欲证明直线GH过定点,只需求出含参数的直线GH的方程,观察是否过定点即可.设出A,B,G,H的坐标,用A,B坐标表示G,H坐标,求出直线GH方程,化为点斜式,可以发现直线必过点(3,0).
,求出a,b,可得双曲线C2的方程;(2)欲证明直线GH过定点,只需求出含参数的直线GH的方程,观察是否过定点即可.设出A,B,G,H的坐标,用A,B坐标表示G,H坐标,求出直线GH方程,化为点斜式,可以发现直线必过点(3,0).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间. 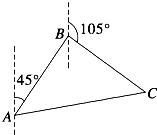
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正项等差数列{an}中a1和a4是方程x2﹣10x+16=0的两个根,若数列{log2an}的前5项和为S5且S5∈[n,n+1],n∈Z,则n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值. 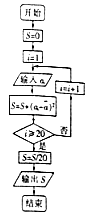
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点D为△ABC的边BC上一点, ![]() =3
=3 ![]() ,En(n∈N+)为边AC上的点,满足
,En(n∈N+)为边AC上的点,满足 ![]() =
= ![]() an+1 ,
an+1 , ![]() =(4an+3)
=(4an+3) ![]() ,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( ) 
A.32n﹣1﹣2
B.2n﹣1
C.4n﹣2
D.24n﹣1﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A、B、C所对的边分别为a、b、c,1+ ![]() =
= ![]() .
.
(1)求A的大小;
(2)若△ABC为锐角三角形,求函数y=2sin2B﹣2cosBcosC的取值范围;
(3)现在给出下列三个条件:①a=1;②2c﹣( ![]() +1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
+1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,(an﹣3)an+1﹣an+4=0(n∈N*).
(1)求a2 , a3 , a4;
(2)猜想{an}的通项公式,并用数学归纳法证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com