【题目】已知离心率为
的椭圆
过点
，点
分别为椭圆的左、右焦点，过
的直线
与
交于
两点，且
.
（1）求椭圆
的方程；
（2）求证：以
为直径的圆过坐标原点.
【答案】（Ⅰ）
（Ⅱ）见解析
【解析】试题分析：
(1)利用离心率结合椭圆所过的点得到关系
的方程组，求解方程组即可求得椭圆的标准方程；
(2)分类讨论，当斜率不存在的时候单独考查，当斜率存在的时候设出直线方程，联立直线与椭圆的方程，结合韦达定理和平面向量的结论证得
即可.
试题解析：
（Ⅰ）点
， 
分别为椭圆的左右焦点，椭圆的方程为
；
由离心率为
得： 
；
过点
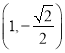得： 
；
所以， 
， 
；椭圆方程为
；
（Ⅱ）由（1）知
， 
；令
， 
；
当直线
的斜率不存在时，直线方程为
；
此时， 
，不满足；设直线方程为
；
代入椭圆方程得： 
韦达定理： 
， 
；
所以， 
，
；
所以， 
；
点
到直线
的距离为
；
所以，由
得： 
；
所以，以
为直径的圆过坐标原点
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】海岛B上有一座高为10米的塔，塔顶的一个观测站A，上午11时测得一游船位于岛北偏东15°方向上，且俯角为30°的C处，一分钟后测得该游船位于岛北偏西75°方向上，且俯角45°的D处（假设游船匀速行驶）．
（1）求该船行驶的速度（单位：米/分钟）．
（2）又经过一段时间后，游船到达海岛B的正西方向E处，问此时游船距离海岛B多远．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】集合M={x|﹣2≤x≤2}，N={y|0≤y≤2}，给出下列四个图形，其中能表示以M为定义域，N为值域的函数关系的是（ ）
A.
B.
C.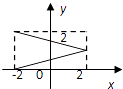
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】共享单车的出现方便了人们的出行，深受我市居民的喜爱．为调查某校大学生对共享单车的使用情况，从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查，得到这100名同学每周使用共享单车的时间（单位：小时）如表：
使用时间 |
|
|
|
|
|
人数 | 10 | 40 | 25 | 20 | 5 |
（Ⅰ）已知该校大一学生由2400人，求抽取的100名学生中大一学生人数；
（Ⅱ）作出这些数据的频率分布直方图；
（Ⅲ）估计该校大学生每周使用共享单车的平均时间
（同一组中的数据用该组区间的中点值作代表）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）=max{x2﹣ax+a，ax﹣a+1}，其中max{x，y}= 
． （Ⅰ）若对任意x∈R，恒有f（x）=x2﹣ax+a，求实数a的值；
（Ⅱ）若a＞1，求f（x）的最小值m（a）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[ 120 , 130），[130 ，140) , [140 , 150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140 ，150]内的学生中选取的人数应为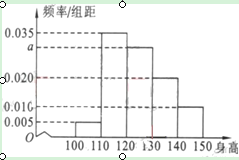 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
