
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
【答案】C
【解析】
试题分析:由于三次函数的三次项系数为正值,当x→-∞时,函数值→-∞,当x→+∞时,函数值也→+∞,又三次函数的图象是连续不断的,故一定穿过x轴,即一定x0∈R,f(x0)=0,选项A中的结论正确;函数f(x)的解析式可以通过配方的方法化为形如(x+m)3+n(x+m)+h的形式,通过平移函数图象,函数的解析式可以化为y=x3+nx的形式,这是一个奇函数,其图象关于坐标原点对称,故函数f(x)的图象是中心对称图形,选项B中的结论正确;由于三次函数的三次项系数为正值,故函数如果存在极值点x1,x2,则极小值点x2>x1,即函数在-∞到极小值点的区间上是先递增后递减的,所以选项C中的结论错误;根据导数与极值的关系,显然选项D中的结论正确.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() )的图象关于点
)的图象关于点![]()
![]() 成中心对称,且与点
成中心对称,且与点![]() 相邻的一个最低点为
相邻的一个最低点为![]() ,则对于下列判断:
,则对于下列判断:
①直线![]() 是函数
是函数![]() 图象的一条对称轴;②函数
图象的一条对称轴;②函数![]() 为偶函数;
为偶函数;
③函数![]() 与
与![]() 的图象的所有交点的横坐标之和为
的图象的所有交点的横坐标之和为![]() .
.
其中正确的判断是__________________.(写出所有正确判断的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列各等式(i为虚数单位):
(cos 1+isin 1)(cos 2+isin 2)=cos 3+isin 3;
(cos 3+isin 3)(cos 5+isin 5)=cos 8+isin 8;
(cos 4+isin 4)(cos 7+isin 7)=cos 11+isin 11;
(cos 6+isin 6)(cos 6+isin 6)=cos 12+isin 12.
记f(x)=cos x+isin x.
猜想出一个用f (x)表示的反映一般规律的等式,并证明其正确性;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() ),其中0<ω<3,已知f(
),其中0<ω<3,已知f( ![]() )=0.(12分)
)=0.(12分)
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)在[﹣
个单位,得到函数y=g(x)的图象,求g(x)在[﹣ ![]() ,
, ![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第二届世界青年奥林匹克运动会,中国获37金,13银,13铜共63枚奖牌居奖牌榜首位,并打破十项青奥会记录.由此许多人认为中国进入了世界体育强国之列,也有许多人持反对意见.有网友为此进行了调查,在参加调查的2 548名男性公民中有1 560名持反对意见,2 452名女性公民中有1 200人持反对意见,在运用这些数据说明中国的奖牌数是否与中国进入体育强国有无关系时,用什么方法最有说服力( )
A. 平均数与方差 B. 回归直线方程
C. 独立性检验 D. 概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为6
之间是正相关还是负相关;若该地1月份某天的最低气温为6![]() ,请用所求回归方程预测该店当日的营业额.
,请用所求回归方程预测该店当日的营业额.
附: 回归方程![]() 中,
中,  ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
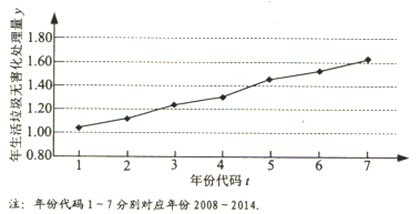
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com