


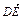 =(-2,4,0),
=(-2,4,0), =(-2,4,0),
=(-2,4,0),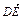 =
= , 4分
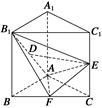
, 4分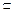 平面ABC,DE
平面ABC,DE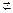 平面ABC.
平面ABC. =(-2,2,-4),
=(-2,2,-4), =(2,-2,-2),
=(2,-2,-2),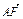 =(2,2,0).
=(2,2,0). ·
· =(-2)×2+2×(-2)+(-4)×(-2)=0,
=(-2)×2+2×(-2)+(-4)×(-2)=0, ⊥
⊥ ,∴B1F⊥EF, 10分
,∴B1F⊥EF, 10分 ·
·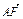 =(-2)×2+2×2+(-4)×0=0.
=(-2)×2+2×2+(-4)×0=0. ⊥
⊥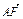 ,即B1F⊥AF, 12分
,即B1F⊥AF, 12分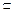 平面ABC,
平面ABC,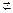 平面ABC,
平面ABC,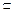 平面B1BF,
平面B1BF, a2,EF2=
a2,EF2= a2,
a2, a2,
a2,

科目:高中数学 来源:不详 题型:解答题
 ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, =
= .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 -ABCD中,侧面PAD为正三角形,底面为正方
-ABCD中,侧面PAD为正三角形,底面为正方| A.椭圆 | B.抛物线 |
| C.双曲线 | D.直线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com