练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知六条桥梁横跨A、B两岸，假设各条桥梁的车流量分别为1,1,2,2,3,4（单位万辆），现从这六条桥梁中任取三条桥梁，考察这三条桥梁的车流量之和
    （1）求的概率    （2）求的概率   （3）求的数学期望
    （1）（2）（3）略
    （1）有两种情况。对应的基本事件数为2
    基本事件总数为 
    （2）对应的基本事件总数为3
    的可能取值为4、5、6、7、8、9

    （3）的分布列为

    		4
    		5
    		6
    		7
    		8
    		9
    P






    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    若一个正态分布的概率密度函数是一个偶函数，且该函数的最大值为.
    （1）求该正态分布的概率密度函数的解析式；
    （2）求正态总体在（-4，4］的概率.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某车站，每天均有3辆客车开往省城，客车分为上、中、下三个等级．某人准备在该车站乘车前往省城办事，但他不知道客车的车况，也不知道发车顺序．为了尽可能乘上上等车，他将采取如下策略：先放过第一辆，如果第二辆比第一辆好，则上第二辆；否则，上第三辆．那么他乘上上等车的概率为           ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题12分）甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.求：（Ⅰ） 打满3局比赛还未停止的概率；（Ⅱ）比赛停止时已打局数为6的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某校在高二年级开设了A，B，C三个兴趣小组，为了对兴趣小组活动的开展情况进行调查，用分层抽样方法从A，B，C三个兴趣小组的人员中，抽取若干人组成调查小组，有关数据见下表（单位：人）
    兴趣小组小组人数抽取人数
    A24x
    B363
    C48y
    （1）求x，y的值；
    （2）若从A，B两个兴趣小组抽取的人中选2人作专题发言，求这2人都来自兴趣小组B的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    一人有n把钥匙，其中只有一把可把房门打开，逐个试验钥匙，房门恰好在第k次被打开（1≤k≤n）的概率是（　　）
    A．
    1
    n!
    		B．
    1
    n
    		C．
    k
    n
    		D．
    1
    (k-1)!n

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    从1，2，3，4，5中随机取出二个不同的数，其和为奇数的概率为（　　）
    A．
    1
    5
    		B．
    2
    5
    		C．
    3
    5
    		D．
    4
    5

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

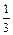    如果X～B(20,), Y～B(20,),那么当X,Y变化时，下面关于P(X=xk)= P(Y=yk)成立的（xk，yk）的个数为（  ）
    A．10B．20C．21D．0

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    已知|x|≤2，|y|≤2，点P的坐标(x，y)
    (1)求当x, y∈R时，P满足(x－2)2+(y－2)2≤4的概率；
    (2)求当x, y∈Z时，P满足(x－2)2+(y－2)2≤4的概率

    查看答案和解析>>

    同步练习册答案