练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．从5位男同学和4位女同学中选出3位同学分别担任数、语、外三科的科代表，要求选出的3位同学中男女都要有，则不同的选派方案共有（　　）
    A．210种B．630种C．420种D．840种

    分析 题目要求有男女同学九人选三个到3个班担任数、语、外三科的科代表是三个元素在九个位置排列，要求这3位班主任中男女同学都有，则选的都是男同学和选的都是女同学不合题意就需要从总数中去掉．

    解答 解：∵共有男女同学九人选三个到3个担任数、语、外三科的科代表共有A93种结果，
    要求这3位班主任中男女同学都有，则选的都是男同学和选的都是女同学不合题意，
    选的都是男同学有A53种结果，
    选的都是女同学有A43种结果，
    ∴满足条件的方案有A93-（A53+A43）=420，
    故选：C．

    点评 排列与组合问题要区分开，若题目要求元素的顺序则是排列问题，排列问题要做到不重不漏，有些题目带有一定的约束条件，解题时要先考虑有限制条件的元素，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．已知△ABC的面积为$\frac{{\sqrt{3}}}{2}$，AC=2，∠BAC=$\frac{π}{3}$，则∠ACB=$\frac{π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1坐标原点为点O，有顶点坐标为（2，0），离心率e=$\frac{{\sqrt{3}}}{2}$，过椭圆右焦点倾斜角为30°的直线交椭圆与点A，B两点．
    （1）求椭圆的方程．
    （2）求三角形OAB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数f（x）=cosx-lnx，实数a，b，c满足f（a）f（b）f（c）＜0（0＜a＜b＜c＜π），若实数x0是f（x）=0的根，那么下列不等式中不可能成立的是（　　）
    A．x0＜cB．x0＞cC．x0＜bD．x0＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

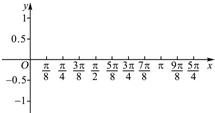    14．设函数f（x）=sin（ωx+φ）（ω＞0，-π＜φ＜0）的两个相邻的对称中心分别为（${\frac{π}{8}$，0），（${\frac{5π}{8}$，0）．
    （Ⅰ）求f（x）的解析式及其对称轴方程；
    （Ⅱ）利用五点法画出函数f（x）在[$\frac{π}{8}$，$\frac{9π}{8}}$]上的简图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在△ABC中，角A，B，C的对边分别是a，b，c，满足2acosC+c=2b．
    （1）求角A的大小；
    （2）若a=1，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．在平面直角坐标系xOy中，已知点A（-1，1），P是动点，且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA．求点P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

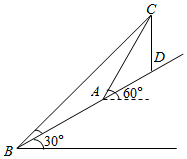    8．如图，要在山坡上A、B两处测量与地面垂直的铁塔CD的高，由A、B两处测得塔顶C的仰角分别为60°和45°，AB长为40m，斜坡与水平面成30°角，则铁塔CD的高为$\frac{40\sqrt{3}}{3}$m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知△ABC的周长为10，且A（-2，0），B（2，0），则C点的轨迹方程是（　　）
    A．$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{9}$=1（y≠0）B．$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1（y≠0）
    C．$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1（y≠0）D．$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1（y≠0）

    查看答案和解析>>

    同步练习册答案