
分析 (Ⅰ)由题意知X可能的取值为0,500,1000,分别求出相应的概率,由此能求出某员工选择方案甲进行抽奖所获奖金X(元)的分布列.
(Ⅱ)求出方案甲抽奖所获奖金X的均值,选择方案乙进行抽奖中奖次数ξ~B(3,$\frac{2}{5}$),从而抽奖所获奖金X′的均值E(X′)=E(400ξ)=400E(ξ)=480,由此得到选择方案甲较划算.
(Ⅲ)选择方案甲不获奖的概率为$\frac{7}{25}$,这些员工不获奖的人数Y~B(100,$\frac{7}{25}$),由此能求出这些员工不获奖的人数.
解答 解:(Ⅰ)由题意知X可能的取值为0,500,1000,(1分)
$P(X=0)=\frac{1}{5}+\frac{4}{5}•\frac{1}{2}•\frac{1}{5}=\frac{7}{25}$,
$P(X=500)=\frac{4}{5}•\frac{1}{2}=\frac{2}{5}$,
$P(X=1000)=\frac{4}{5}•\frac{1}{2}•\frac{4}{5}=\frac{8}{25}$(4分)
所以某员工选择方案甲进行抽奖所获奖金X(元)的分布列为
| X | 0 | 500 | 1000 |
| P | $\frac{7}{25}$ | $\frac{2}{5}$ | $\frac{8}{25}$ |
点评 本题考查离散型随机变量的分布列及数学期望的求法及应用,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-e | B. | a>1 | C. | a>e | D. | a<-3或a>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
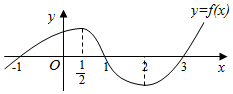
| A. | $(-∞,\frac{1}{2})∪(\frac{1}{2},2)$ | B. | (-1,0)∪(1,3) | C. | $(-∞,\frac{1}{2})∪(\frac{1}{2},+∞)$ | D. | $(-∞,\frac{1}{2})∪(2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 49 | B. | $\frac{1}{{4}^{6}}$ | C. | $\frac{1}{{4}^{6}}$或49 | D. | -49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(x≠0) | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(x≠0) | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(y≠0) | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(y≠0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com