
【题目】已知函数![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)求![]() 在区间
在区间![]() 上对称轴、对称中心及其最值.
上对称轴、对称中心及其最值.
【答案】(1)最小正周期为![]() (2)对称轴
(2)对称轴![]() ,对称中心为
,对称中心为![]() ,最大值为
,最大值为![]() ,最小值为
,最小值为![]()
【解析】
(1)根据同角三角函数关系式的平方和关系、降幂公式、辅助角公式把函数的解析式化简成正弦型函数解析形式,最后根据最小正周期公式求出函数的最小正周期;
(2)利用正弦型函数的对称性和单调性,求出![]() 在区间
在区间![]() 上对称轴、对称中心及其最值
上对称轴、对称中心及其最值
解:(1)因为![]()
![]()
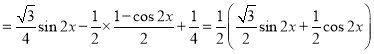
![]() ,
,
所以,函数![]() 的最小正周期为
的最小正周期为![]() .
.
(2)由(1)知![]() ,
,
因为![]() ,所以
,所以![]() ,①
,①
令![]() ,得
,得![]() ,
,
所以![]() ,即为所求函数
,即为所求函数![]() 在
在![]() 上的对称轴;
上的对称轴;
令![]() ,得
,得![]() ,所以
,所以![]() ,
,
所以函数![]() 在
在![]() 上的对称中心为
上的对称中心为![]() ;(*)
;(*)
易判断函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递增.
上单调递增.
所以,![]() ,
,![]() ,
,![]() ,
,
故函数![]() 在区间
在区间![]() 上最大值为
上最大值为![]() ,最小值为
,最小值为![]() .
.
【另解】
接(*)式
由①得![]() ,所以
,所以![]() ,
,
故函数![]() 在区间
在区间![]() 上最大值为
上最大值为![]() ,最小值为
,最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
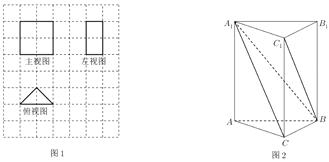
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
(2)在堑堵![]() 中,如图2,
中,如图2,![]() ,若
,若![]() ,当阳马
,当阳马![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且满足:
且满足:![]()
(1)证明:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式.
的通项公式.
(2)设![]() ,若数列
,若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)在(2)的条件下,设![]() 记数列
记数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 存在实数
存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知某公园的四处景观分别位于等腰梯形![]() 的四个顶点处,其中
的四个顶点处,其中![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() .现拟规划在
.现拟规划在![]() (不包括端点)路段上增加一个景观
(不包括端点)路段上增加一个景观![]() ,并建造观光路直接通往
,并建造观光路直接通往![]() 处,造价为每千米
处,造价为每千米![]() 万元,又重新装饰
万元,又重新装饰![]() 路段,造价为每千米
路段,造价为每千米![]() 万元.
万元.
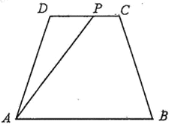
(1)若拟修建观光路![]() 路段长为
路段长为![]() 千米,求
千米,求![]() 路段的造价;
路段的造价;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,
,![]() 段的总造价最低.
段的总造价最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]() ,
,![]() 为异面直线; ②若
为异面直线; ②若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,则
,则![]() ; ④若
; ④若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
则上述命题中真命题的序号为( )
A.①②B.③④C.②D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击小组有甲、乙、丙三名射手,已知甲击中目标的概率是![]() ,甲、丙二人都没有击中目标的概率是
,甲、丙二人都没有击中目标的概率是![]() ,乙、丙二人都击中目标的概率是
,乙、丙二人都击中目标的概率是![]() .甲乙丙是否击中目标相互独立.
.甲乙丙是否击中目标相互独立.
(1)求乙、丙二人各自击中目标的概率;
(2)设乙、丙二人中击中目标的人数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com