
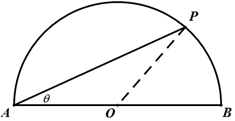
 运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.
运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.分析 (1)求出∠POB的弧度,从而求出PB的长度即可;
(2)根据PB的长,求出t(θ)的解析式即可;(3)求出函数的导数,根据函数的单调性求出t(θ)的最大值,带入计算比较即可.
解答 解:(1)∵$∠POB=2θ=\frac{π}{3}$,
∴$\widehat{PB}=OA•\frac{π}{3}=500π$m.
(2)在OAP中,AP=2OAcosθ=3000cosθ,
在扇形OPB中,$\widehat{PB}=OA•(2θ)=3000θ$,
又BA=2OA=3000,
∴小王本次训练的总时间:
$t(θ)=\frac{AP}{2}+\frac{{\widehat{PB}}}{4}+\frac{BA}{10}=\frac{3000cosθ}{2}+\frac{3000θ}{4}+\frac{3000}{10}$
=$1500(cosθ+\frac{θ}{2})+300$,$θ∈(0,\frac{π}{2})$,
(3)由(2)得:$t'(θ)=-1500(sinθ-\frac{1}{2})$,
令t'(θ)=0,得$sinθ=\frac{1}{2}$,∴$θ=\frac{π}{6}$,
列表如下,
| θ | $(0,\frac{π}{6})$ | $\frac{π}{6}$ | $(\frac{π}{6},\frac{π}{2})$ |
| t'(θ) | + | 0 | - |
| t(θ) | ↗ | 极大值 | ↘ |
点评 本题考查了弧长公式,考查函数的单调性、最值问题,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y2=±2$\sqrt{2}$x | B. | y2=±2x | C. | y2=±4x | D. | y2=±4$\sqrt{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y+5=0 | B. | x-2y+5=0 | C. | $2x+y+5\sqrt{5}=0$ | D. | $x-2y+5\sqrt{5}=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{17}$ | B. | $\frac{14}{17}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-48,0) | C. | (-192,0) | D. | (-60,-48) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com