
【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数![]() 为基本素材,研究该函数的相关性质,取得部分研究成果如下:
为基本素材,研究该函数的相关性质,取得部分研究成果如下:
①同学甲发现:函数![]() 的定义域为
的定义域为![]() ;
;
②同学乙发现:函数![]() 是偶函数;
是偶函数;
③同学丙发现:对于任意的![]() 都有
都有![]() ;
;
④同学丁发现:对于任意的![]() ,都有
,都有![]() ;
;
⑤同学戊发现:对于函数![]() 定义域中任意的两个不同实数
定义域中任意的两个不同实数![]() ,总满足
,总满足![]() .
.
其中所有正确研究成果的序号是__________.
科目:高中数学 来源: 题型:
【题目】随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p1,点数之和大于5的概率记为p2,点数之和为偶数的概率记为p3,则
( )
A. p1<p2<p3 B. p2<p1<p3 C. p1<p3<p2 D. p3<p1<p2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据画出2×2列联表;
(2)请问能有多大把握认为药物有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面(A)(B)(C)(D)为四个平面图形: 
(1)数出每个平面图形的交点数、边数、区域数,并将下表补充完整:
交点数 | 边数 | 区域数 | |
(A) | 4 | 5 | 2 |
(B) | 5 | 8 | |
(C) | 12 | 5 | |
(D) | 15 |
(2)观察表格,若记一个平面图形的交点数、边数、区域数分别为E、F、G,试猜想E、F、G之间的数量关系(不要求证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…,(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 ![]() =
= ![]() x+
x+ ![]() 必过样本中心(
必过样本中心( ![]() ,
, ![]() )
)
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.若“p且q”为假,则p,q至少有一个是假命题
B.命题“x∈R,x2﹣x﹣1<0”的否定是““x∈R,x2﹣x﹣1≥0”
C.当a<0时,幂函数y=xa在(0,+∞)上单调递减
D.“φ= ![]() ”是“y=sin(2x+φ)为偶函数”的充要条件
”是“y=sin(2x+φ)为偶函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立坐标系.已知曲线C:ρsin2θ=2acosθ(a>0),过点P(﹣2,﹣4)的直线l的参数方程为 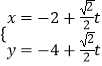 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.
(1)写出曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若f(x)满足条件:存在[a,b]D,使f(x)在[a,b]上的值域是[ ![]() ,
, ![]() ],则成f(x)为“倍缩函数”,若函数f(x)=log2(2x+t)为“倍缩函数”,则t的范围是( )
],则成f(x)为“倍缩函数”,若函数f(x)=log2(2x+t)为“倍缩函数”,则t的范围是( )
A.(0, ![]() )
)
B.(0,1)
C.(0, ![]() ]
]
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com