
���� ���ݳ���Ժͱ�Ҫ�ԵĶ���֤���жϼ��ɣ�
��� �⣺������$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$=��
��x1=��x2��y1=��y2��z1=��z2��
��$\overrightarrow{a}$=��x1��y1��z1��=�ˣ�x2��y2��z2��=��$\overrightarrow{b}$��
������$\overrightarrow{a}$��$\overrightarrow{b}$���ߣ�
������x1=0��y2=y1��z2=z1��������$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$����Ҫ�Բ�������
�����dz�ֲ���Ҫ������
���� ���⿼���˳�����Ҫ�������ж����⣬Ҳ�����˿ռ�������Ӧ�����⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ�� | B�� | ���� | C�� | һ�������� | D�� | ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
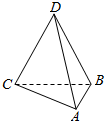 ��֪��ͼ��ʾ������D-ABC���ĸ����������O�������ϣ���ABC�͡�DBC����ƽ�����ֱ��AB=3��AC=$\sqrt{3}$��BC=CD=BD=2$\sqrt{3}$������O�ı����Ϊ��������
��֪��ͼ��ʾ������D-ABC���ĸ����������O�������ϣ���ABC�͡�DBC����ƽ�����ֱ��AB=3��AC=$\sqrt{3}$��BC=CD=BD=2$\sqrt{3}$������O�ı����Ϊ��������| A�� | 4�� | B�� | 12�� | C�� | 16�� | D�� | 36�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��-2 | B�� | a��-2 | C�� | a��2 | D�� | a��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-9��9] | B�� | [-12��12] | C�� | [-15��15] | D�� | [-18��18] |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com