
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 为菱形,
为菱形,![]() 为
为![]() 的中点,
的中点,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,且
,且![]() .
.
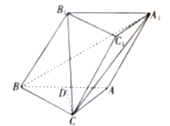
(1)证明:![]() 平面
平面![]() .
.
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若在区间![]() 上存在不相等的实数
上存在不相等的实数![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)设![]() 的图象为
的图象为![]() ,
,![]() 的图象为
的图象为![]() ,若直线
,若直线![]() 与
与![]() 分别交于
分别交于![]() ,问是否存在整数
,问是否存在整数![]() ,使
,使![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线互相平行,若存在,求出
处的切线互相平行,若存在,求出![]() 的所有值,若不存在,请说明理由.
的所有值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】货车欲以xkm/h的速度行驶,去130km远的某地,按交通法规,限制x的允许范围是50≤x≤100,假设汽油的价格为2元/升,而汽车耗油的速率是![]() 升/小时.司机的工资是14元/小时,试问最经济的车速是多少?这次行车往返的总费用最低是多少?
升/小时.司机的工资是14元/小时,试问最经济的车速是多少?这次行车往返的总费用最低是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() ,
,![]() 平面
平面![]() ,P是
,P是![]() 内一点,点E,F在直线
内一点,点E,F在直线![]() 上运动,若直线
上运动,若直线![]() 和
和![]() 所成角的最小值与直线
所成角的最小值与直线![]() 和平面
和平面![]() 所成角的最大值相等,则满足条件的点P的轨迹是( )
所成角的最大值相等,则满足条件的点P的轨迹是( )
A.圆的一部分B.椭圆的一部分C.抛物线的一部分D.双曲线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com