
【题目】
已知曲线![]() 上的点到点
上的点到点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2.
的距离小2.
(1)求曲线![]() 的方程;
的方程;
(2)曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 分别与直线
分别与直线![]() 及
及![]() 轴交于点
轴交于点![]() ,以
,以![]() 为直径作圆
为直径作圆![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,试探究:当点
,试探究:当点![]() 在曲线
在曲线![]() 上运动(点
上运动(点![]() 与原点不重合)时,线段
与原点不重合)时,线段![]() 的长度是否发生变化?证明你的结论.
的长度是否发生变化?证明你的结论.
【答案】(1)![]() .(2)当点P在曲线
.(2)当点P在曲线![]() 上运动时,线段AB的长度不变,证明见解析.
上运动时,线段AB的长度不变,证明见解析.
【解析】
试题(1)思路一:设![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,
依题意可知曲线![]() 是以点
是以点![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,
为准线的抛物线,
得到曲线![]() 的方程为
的方程为![]() .
.
思路二:设![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,
由![]() ,化简即得.
,化简即得.
(2)当点P在曲线![]() 上运动时,线段AB的长度不变,证明如下:
上运动时,线段AB的长度不变,证明如下:
由(1)知抛物线![]() 的方程为
的方程为![]() ,
,
设![]() ,得
,得![]() ,
,
应用导数的几何意义,确定切线的斜率,进一步得切线![]() 的方程为
的方程为![]() .
.
由 ,得
,得![]() .
.
由 ,得
,得![]() .
.
根据![]() ,得圆心
,得圆心![]() ,半径
,半径 ,
,
由弦长,半径及圆心到直线的距离之关系,确定![]() .
.
试题解析:解法一:(1)设![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,
依题意,点S到![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等,
的距离相等,
所以曲线![]() 是以点
是以点![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,
为准线的抛物线,
所以曲线![]() 的方程为
的方程为![]() .
.
(2)当点P在曲线![]() 上运动时,线段AB的长度不变,证明如下:
上运动时,线段AB的长度不变,证明如下:
由(1)知抛物线![]() 的方程为
的方程为![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() ,得切线
,得切线![]() 的斜率
的斜率
![]() ,
,
所以切线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由 ,得
,得![]() .
.
由 ,得
,得![]() .
.
又![]() ,所以圆心
,所以圆心![]() ,
,
半径 ,
,
 .
.
所以点P在曲线![]() 上运动时,线段AB的长度不变.
上运动时,线段AB的长度不变.

解法二:
(1)设![]() 为曲线
为曲线![]() 上任意一点,
上任意一点,
则![]() ,
,
依题意,点![]() 只能在直线
只能在直线![]() 的上方,所以
的上方,所以![]() ,
,
所以![]() ,
,
化简得,曲线![]() 的方程为
的方程为![]() .
.
(2)同解法一.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的“局部对称点”.
的“局部对称点”.
(1)![]() ,其中
,其中![]() ,试判断
,试判断![]() 是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
(2)若函数![]() 在区间
在区间![]() 内有“局部对称点”,求实数m的取值范围;
内有“局部对称点”,求实数m的取值范围;
(3)若函数![]() 在R上有“局部对称点”,求实数m的取值范围.
在R上有“局部对称点”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
![]()
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前,100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
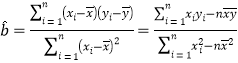 ,参考数值:
,参考数值:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
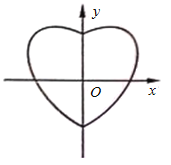
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数![]() ,给出下列命题:①“
,给出下列命题:①“![]() ”是“
”是“![]() ”的充要条件;②“
”的充要条件;②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;③“
是无理数”的充要条件;③“![]() ”是“
”是“![]() ”的充分条件;④“
”的充分条件;④“![]() ”是“
”是“![]() ”的必要条件;其中真命题的个数是( )
”的必要条件;其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com