
【题目】如图所示,椭圆![]() ,
,![]() 、
、![]() ,为椭圆
,为椭圆![]() 的左、右顶点.
的左、右顶点.

![]() 设
设![]() 为椭圆
为椭圆![]() 的左焦点,证明:当且仅当椭圆
的左焦点,证明:当且仅当椭圆![]() 上的点
上的点![]() 在椭圆的左、右顶点时,
在椭圆的左、右顶点时,![]() 取得最小值与最大值.
取得最小值与最大值.
![]() 若椭圆
若椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() ,最小值为
,最小值为![]() ,求椭圆
,求椭圆![]() 的标准方程.
的标准方程.
![]() 若直线
若直线![]() 与
与![]() 中所述椭圆
中所述椭圆![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不是左、右顶点),且满足
不是左、右顶点),且满足![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
【答案】![]() 见解析;
见解析;![]()
![]() ;
;![]() 见解析,
见解析,![]() .
.
【解析】
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,令
,令![]() ,由点
,由点![]() 在椭圆
在椭圆![]() 上,得
上,得![]() ,
,
则![]() ,代入式子,利用二次函数的性质和
,代入式子,利用二次函数的性质和![]() 的取值范围,求出函数的最值以及对应的
的取值范围,求出函数的最值以及对应的![]() 的取值,即可求证;
的取值,即可求证;
![]() 由已知与
由已知与![]() ,得
,得![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,再由
,再由![]() 求出
求出![]() ,进而求出椭圆的标准方程;
,进而求出椭圆的标准方程;
![]() 假设存在满足条件的直线,设
假设存在满足条件的直线,设![]() ,
,![]() ,联立直线方程和椭圆方程进行整理,化简出一元二次方程,再利用韦达定理列出方程组,根据题意得
,联立直线方程和椭圆方程进行整理,化简出一元二次方程,再利用韦达定理列出方程组,根据题意得![]() ,代入列出关于
,代入列出关于![]() 的方程,进行化简求解.
的方程,进行化简求解.
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,令
,令![]() .
.
由点![]() 在椭圆
在椭圆![]() 上,得
上,得![]() ,
,
则![]() ,代入
,代入![]() ,
,
得![]() ,
,
其对称轴方程为![]() ,
,
由题意,知![]() 恒成立,
恒成立,
![]()
![]() 在区间
在区间![]() 上单调递增.
上单调递增.
当且仅当椭圆![]() 上的点
上的点![]() 在椭圆的左、右顶点时,
在椭圆的左、右顶点时,![]() 取得最小值与最大值.
取得最小值与最大值.
![]() 由已知与
由已知与![]() ,得
,得![]() ,
,![]() ,
,
![]()
![]() ,
,![]() .
.![]()
![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
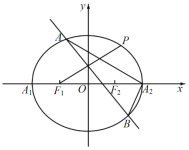
![]() 如图所示,设
如图所示,设![]() ,
,![]() ,
,
联立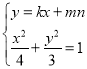 ,得
,得![]() ,
,
![]()
则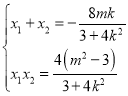
则![]()
![]()
![]()
![]() 椭圆的右顶点为
椭圆的右顶点为![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
即![]() .
.
![]() .
.
![]()
![]() ,
,
解得![]() ,
,![]() ,且均满足
,且均满足![]() .
.
当![]() 时,l的方程为
时,l的方程为![]() 直线过定点
直线过定点![]() ,与已知矛盾.
,与已知矛盾.
当![]() 时,l的方程为
时,l的方程为![]() 直线过定点
直线过定点![]() ,满足题意,
,满足题意,
![]() 直线l过定点,定点坐标为
直线l过定点,定点坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】某国营企业集团公司现有员工1000名,平均每人每年创造利润10万元.为了激化内部活力,增强企业竞争力,集团公司董事会决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业;调整后,他们平均每人每年创造利润
)名员工从事第三产业;调整后,他们平均每人每年创造利润![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() %.
%.
(Ⅰ)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(Ⅱ)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则实数![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,某校在高中生中随机抽取100名学生进行了问卷调查,得到如下列联表:
喜欢数学 | 不喜欢数学 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 50 | 100 |
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.001的前提下认为“喜欢数学”与性别有关?说明你的理由;
(3)若在接受调查的所有男生中按照“是否喜欢数学”进行分层抽样,现随机抽取6人,再从6人中抽取3人,求至少有1人“不喜欢数学”的概率.
下面的临界值表供参考:
| 0.05 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式: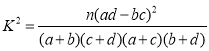 ,其中
,其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 后,与曲线
后,与曲线![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若S![]() 是公差不为0的等差数列
是公差不为0的等差数列![]() 的前
的前![]() 项和,且
项和,且![]() 成等比数列。
成等比数列。
(1)求等比数列![]() 的公比;
的公比;
(2)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)设![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,求使得
项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数
都成立的最小正整数![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 30 | 45 |
很满意 | 25 | 10 | 35 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有99%的把握认为满意程度与年龄有关?
(2)为了帮助年龄在40岁以下的未购房的8名员工解决实际困难,该企业拟员工贡献积分![]() (单位:分)给予相应的住房补贴
(单位:分)给予相应的住房补贴![]() (单位:元),现有两种补贴方案,方案甲:
(单位:元),现有两种补贴方案,方案甲:![]() ;方案乙:
;方案乙: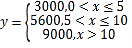 .已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“
.已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“![]() 类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“
类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“![]() 类员工”的概率。
类员工”的概率。
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体QPABCD为一简单组合体,在底面ABCD中,∠DAB=60°,AD⊥DC,AB⊥BC,QD⊥平面ABCD,PA∥QD,PA=1,AD=AB=QD=2.

(1)求证:平面PAB⊥平面QBC;
(2)求该组合体QPABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com