
【题目】某工厂拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为![]() 米,高为
米,高为![]() 米,体积为
米,体积为![]() 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为![]() 元(
元(![]() 为圆周率).该蓄水池的体积最大时
为圆周率).该蓄水池的体积最大时![]() ______.
______.
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是中国古代的著名数学著作,该书表明:至迟于公元5世纪,中国已经系统掌握等差数列的相关理论,该书上卷22题又“女工善织问题”:“今有女善织,日益功疾,初日织五尺,今一月曰织九匹三丈,问日益几何?”,大概意思是:有一个女工人善于织布,每天织布的尺数越来越多且成等差数列,第一天知5尺,30天共织九匹三丈,问每天增加的织布数目是多少寸?答案是__________寸.(注:当时一匹为四丈,一丈为十尺,一尺为十寸,结果四舍五入精确到寸)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】坐标系与参数方程:在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上
上
(Ⅰ)求![]() 的值和直线
的值和直线![]() 的直角坐标方程及
的直角坐标方程及![]() 的参数方程;
的参数方程;
(Ⅱ)已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),直线
为参数),直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的所有棱长都为
的所有棱长都为![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 在
在![]() 边上,
边上,![]() .
.
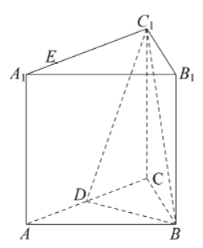
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是侧面
是侧面![]() 内的动点,且
内的动点,且![]() 平面
平面![]() .
.
①在答题卡中作出点![]() 的轨迹,并说明轨迹的形状(不需要说明理由);
的轨迹,并说明轨迹的形状(不需要说明理由);
②求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,△PAB是边长为2的等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,BC=CD=1,PD![]() .
.
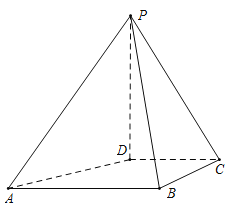
(1)证明:AB⊥PD.
(2)求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年中各月份的收入、支出情况的统计如图所示,下列说法中正确的是______.
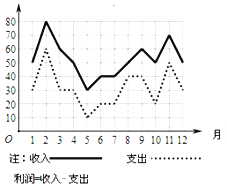
①2至3月份的收入的变化率与11至12月份的收入的变化率相同;
②支出最高值与支出最低值的比是6:1;
③第三季度平均收入为50万元;
④利润最高的月份是2月份。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿着
沿着![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,如图2.
,如图2.
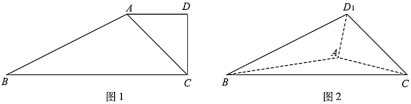
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com