练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数f(x)＝A·tan(ωx+φ)(φ＞0)在区间[m，n]上的函数值都小于0，则函数g(x)＝A·cot(ωx+φ)在[m，n]上的函数值
    A．都大于0，且有最大值为g(m)B．都小于0，且有最大值为g(m)
    C．都大于0，且有最小值为g(m)D．都小于0，且有最小值为g(m)
    B
    因仍负可排除（A）（C），由A＞0时递增可知递减，从而选（B）或取A＝ω＝1，φ＝，，而得（B）
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    某“帆板”集训队在一海滨区域进行集训，该海滨区域的海浪高度（米）随着时间而周期性变化，每天各时刻的浪高数据的平均值如下表：

    		0
    		3
    		6
    		9
    		12
    		15
    		18
    		21
    		24

    		1.0
    		1.4
    		1.0
    		0.6
    		1.0
    		1.4
    		0.9
    		0.5
    		1.0
    小题1:试画出散点图；
    小题2:观察散点图，从中选择一个合适的函数模型，并求出该拟合模型的解析式；
    小题3:如果确定在白天7时~19时当浪高不低于0.8米时才进行训练，试安排恰当的训练时间.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数（其中）的图象与x轴在原点右侧的第一个交点为N（6，0），又（1）求这个函数解析式（2）设关于x的方程在[0，8]内有两个不同根，求的值及k的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分15分）在△中，内角、、所对的边分别是、、，已知，，（1）若，求、的值；（2）若角为锐角，设，△的周长为，试求函数的最大值.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题12分）画出函数的图象。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

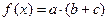    设函数，其中向量，，
    ，。
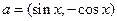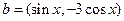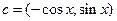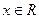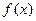    （1）求函数的最大值和最小正周期；
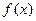    （2）将函数的图像按向量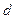平移，使平移后得到的图像关于坐标原点成中心对称，求长度最小的。

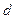    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数的最小正周期为(     )
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设和
    求的值.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知函数y=sin（x+）（>0, -<）的图像如图所示，则 ="________________  "

    查看答案和解析>>

    同步练习册答案