
【题目】已知函数![]() ,其中
,其中![]() 是自然数的底数,
是自然数的底数,![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() ,试判断
,试判断![]() 在
在![]() 上是否有最大或最小值,说明你的理由.
上是否有最大或最小值,说明你的理由.
【答案】(1)![]() ;(2)
;(2)![]() 在
在![]() 上有最小值,无最大值.
上有最小值,无最大值.
【解析】
试题分析:(1)由于![]() ,因此不等式
,因此不等式![]() 可化为二次不等式
可化为二次不等式![]() ,利用二次不等式的解的结论可得;(2)判断最大值和最小值,首先研究函数的单调性,即求出
,利用二次不等式的解的结论可得;(2)判断最大值和最小值,首先研究函数的单调性,即求出![]() ,考虑
,考虑![]() 的解,如有解,判断这个解是否在
的解,如有解,判断这个解是否在![]() 上,从而确定函数在
上,从而确定函数在![]() 上的单调性,本题中判断解的情况可利用二次函数
上的单调性,本题中判断解的情况可利用二次函数![]() 的性质,判断出导函数在
的性质,判断出导函数在![]() 内有一个零点,记为
内有一个零点,记为![]() ,再判断导函数的正负,有结论在在
,再判断导函数的正负,有结论在在![]() 上
上![]() ,
,![]() 递减,在
递减,在![]() 上
上![]() ,
,![]() 递增,从而
递增,从而![]() 在
在![]() 上有最小值,无最大值.
上有最小值,无最大值.
试题解析:(1)因为![]() ,所以不等式
,所以不等式![]() 即为
即为![]() ,
,
又因为![]() ,所以不等式可化为
,所以不等式可化为![]() ,
,
所以不等式![]() 的解集为
的解集为![]() .
.
(2)![]() ,
,
令![]() ,
,
图象对称轴为![]() .
.
因为![]() ,所以
,所以![]() 在
在![]() 内有零点,记为
内有零点,记为![]() ,
,
在![]() 上
上![]() ,
,![]() 递减,在
递减,在![]() 上
上![]() ,
,![]() 递增,
递增,
![]() 在
在![]() 上有最小值,无最大值.
上有最小值,无最大值.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1经过两点(-1,-2),(-1,4),直线l2经过两点(2,1),(6,y),且l1⊥l2,则y=( )
A. -2 B. 1 C. 2 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
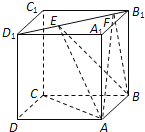
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.
(1)记甲班“口语王”人数为![]() ,乙班“口语王”人数为
,乙班“口语王”人数为![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.
(2)随机从“口语王”中选取2人,记![]() 为来自甲班“口语王”的人数,求
为来自甲班“口语王”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com