
【题目】为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 2 | 4 | 8 | 4 | 2 |
男生:
睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
人数 | 1 | 5 | 6 | 5 | 3 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
男生 | |||
女生 | |||
合计 |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
【答案】
(1)
解:选取的20名女生中,“睡眠严重不足”的有2人,设为A、B,
睡眠时间在[5,6)的有4人,设为a、b、c、d;
从中选取2人的情况有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd共15种,
其中恰有1人“睡眠严重不足”的有AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd共8种,
因此2人中恰有一个为“严重睡眠不足”的概率为P= ![]()
(2)
解:填写2×2列联表如下;
睡眠少于7小时 | 睡眠不少于7小时 | 合计 | |
男生 | 12 | 8 | 20 |
女生 | 14 | 6 | 20 |
合计 | 26 | 14 | 40 |
计算观测值,得 ![]() ,
,
对照数表,得出没有90%的把握认为“睡眠时间与性别有关”
【解析】(1)利用列举法求出基本事件数以及对应事件的概率;(2)填写2×2列联表,根据公式计算观测值,对照数表得出统计结论.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PC=5,PB=4,AB=BC=2 ![]() ,∠ACB=30°.
,∠ACB=30°. 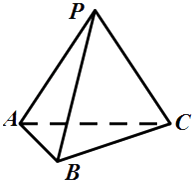
(1)求证:AC⊥PB;
(2)求三棱锥P﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在直线y=4x上,且与直线l:x+y﹣2=0相切于点P(1,1).
(1)求圆的方程;
(2)直线kx﹣y+3=0与该圆相交于A、B两点,若点M在圆上,且有向量 ![]() (O为坐标原点),求实数k.
(O为坐标原点),求实数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+1|﹣|x﹣4|.
(1)解不等式f(x)>0;
(2)若f(x)+3|x﹣4|>m对一切实数x均成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在体积为72的直三棱柱ABC﹣A1B1C1中,AB=3,AC=4,AA1=12. 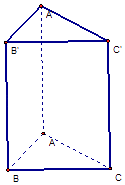
(1)求角∠BAC的大小;
(2)若该三棱柱的六个顶点都在球O的球面上,求球O的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(m﹣2)
=(m﹣2) ![]() +2
+2 ![]() ,
, ![]() =
= ![]() +(m+1)
+(m+1) ![]() ,其中
,其中 ![]() 、
、 ![]() 分别为x、y轴正方向单位向量.
分别为x、y轴正方向单位向量.
(1)若m=2,求 ![]() 与
与 ![]() 的夹角;
的夹角;
(2)若( ![]() +
+ ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),求实数m的值.
),求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com