
分析 对函数f(x)=2x4-10x2+2x-1进行求导,求得函数的极值,单调性,判断零点个数,对于函数g(x)=2xn+10x2-2x-1(n≥3,n∈N)用同样的方法可得,注意计算时整体代换.
解答 解:∵函数f(x)=2x4-10x2+2x-1
∴f′(x)=8x3-20x+2=2(4x3-10x+1)
在f′(x)=0时,
f(x)=2x4-10x2+2x-1,
=2x4-5x2+$\frac{1}{2}$x-5x2+$\frac{3}{2}$x-1,
=$\frac{1}{2}$(4x3-10x+1)-5x2+$\frac{3}{2}$x-1,
=-5x2+$\frac{3}{2}$x-1,
由于判别式△<0,
∴f(x)的所有极值均是负数.
又∵当x趋向于负无穷和正无穷时均为无穷大,
∴零点有两个.
g(x)=2xn+10x2-2x-1(n>3,n∈N且n为奇数)
也有,g′(x)=0时有,g(x)=($\frac{20}{n}$-10)x2+(2-$\frac{2}{n}$)x-1
可知n>3时,其判别式△<0
n为奇数时,有3个零点,
故答案为:3.
点评 考查函数零点判定定理和利用导数研究函数的单调性和极值等问题,同时考查学生灵活应用知识分析解决问题的能力和计算能力,属于中档题.


 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
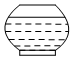 一个高为H,容积为V的鱼缸的轴截面如图所示,向鱼缸里注水,若鱼缸里的水面高度为h时,鱼缸里的水的体积为V',则函数V'=f(h)的大致图象可能是( )
一个高为H,容积为V的鱼缸的轴截面如图所示,向鱼缸里注水,若鱼缸里的水面高度为h时,鱼缸里的水的体积为V',则函数V'=f(h)的大致图象可能是( )| A. | 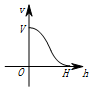 | B. | 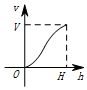 | C. | 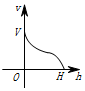 | D. | 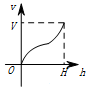 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com