
分析 (1)$\sqrt{{x}^{2}+{y}^{2}}$表示(x,y)与原点的距离,由于圆心(2,0)到原点的距离为2,圆的半径为$\sqrt{3}$,可得$\sqrt{{x}^{2}+{y}^{2}}$的最大值和最小值;
(2)设k=$\frac{y}{x}$,即kx-y=0,利用直线和圆的位置关系即可得到结论.
解答 解:(1)$\sqrt{{x}^{2}+{y}^{2}}$表示(x,y)与原点的距离,由于圆心(2,0)到原点的距离为2,圆的半径为$\sqrt{3}$,
∴$\sqrt{{x}^{2}+{y}^{2}}$的最大值为2+$\sqrt{3}$,最小值为2-$\sqrt{3}$;
(2)设k=$\frac{y}{x}$,即kx-y=0,
则圆心到直线的距离d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$≤$\sqrt{3}$,
解得-$\sqrt{3}$≤k≤$\sqrt{3}$,
故$\frac{y}{x}$的最大值是$\sqrt{3}$,最小值为-$\sqrt{3}$.
点评 本题主要考查直线和圆的方程的应用,根据圆心到直线的距离和半径之间的关系是解决本题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
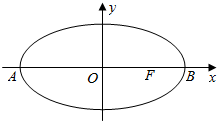 在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
在平面直角坐标系xOy中,如图,已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com