
分析 由条件x+y=2得$\frac{2x+4y}{6}$+$\frac{x-y}{6}$=1,利用1的代换,结合基本不等式的性质进行求解即可.
解答 解:∵x+y=2,
∴3x+3y=6,
即2x+4y+x-y=6,
则$\frac{2x+4y}{6}$+$\frac{x-y}{6}$=1,
∵实数x,y满足x>y>0,∴x-y>0,
则$\frac{1}{2x+4y}$+$\frac{2}{x-y}$=($\frac{1}{2x+4y}$+$\frac{2}{x-y}$)($\frac{2x+4y}{6}$+$\frac{x-y}{6}$)=$\frac{1}{6}$+$\frac{2}{6}$+$\frac{2x+4y}{3(x-y)}$+$\frac{x-y}{6(2x+4y)}$≥$\frac{1}{2}$+2$\sqrt{\frac{2x+4y}{3(x-y)}•\frac{x-y}{6(2x+4y)}}$=$\frac{1}{2}+2×\frac{\sqrt{2}}{6}$=$\frac{1}{2}+\frac{\sqrt{2}}{3}$,
当且仅当$\frac{2x+4y}{3(x-y)}$=$\frac{x-y}{6(2x+4y)}$时,取等号,
故$\frac{1}{2x+4y}$+$\frac{2}{x-y}$的最小值为$\frac{1}{2}+\frac{\sqrt{2}}{3}$,
故答案为:$\frac{1}{2}+\frac{\sqrt{2}}{3}$
点评 本题主要考查不等式最值的求解,根据条件转化为基本不等式形式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
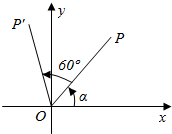 如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).
如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | 1或3 | C. | 2或3 | D. | 3或6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
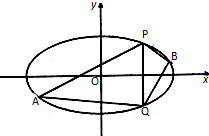 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}$y的焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com