Question

5．已知△ABC是边长为$2\sqrt{3}$的正三角形，EF为△ABC的外接圆o的一条直径，M为△ABC的边上的动点，则$\overrightarrow{ME}•\overrightarrow{MF}$的最小值为-3．

Answer 1

分析 建立平面直角坐标系，对点M的取值情况分在AB、BC和AC上三种情形进行讨论，再求其最小值即可．

解答 解：如图所示，以边AB所在直线为x轴，以其中点为坐标原点建立平面直角坐标系，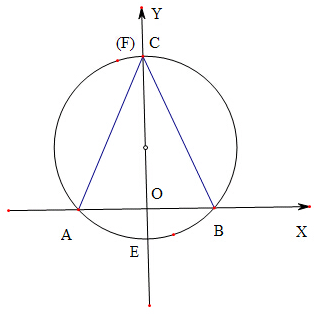
∵该正三角形ABC的边长为2$\sqrt{3}$，
∴A（-$\sqrt{3}$，0），B（$\sqrt{3}$，0），C（0，3），
E（0，-1），F（0，3），
当点M在边AB上时，设点M（x₀，0），则
-$\sqrt{3}$≤x₀≤$\sqrt{3}$，$\overrightarrow{ME}$=（-x₀，-1），
$\overrightarrow{MF}$=（x₀，-3），
∴$\overrightarrow{ME}$•$\overrightarrow{MF}$=-x₀²+3，
∵-$\sqrt{3}$≤x₀≤$\sqrt{3}$，
∴$\overrightarrow{ME}$•$\overrightarrow{MF}$的最小值为0；
当点M在边BC上时，
∵直线BC的斜率为-$\sqrt{3}$，
∴直线BC的方程为：$\sqrt{3}$x+y-3=0，
设点M（x₀，3-$\sqrt{3}$x₀），
则0≤x₀≤$\sqrt{3}$，
∵$\overrightarrow{ME}$=（-x₀，$\sqrt{3}$x₀-4），$\overrightarrow{MF}$=（-x₀，$\sqrt{3}$x₀），
∴$\overrightarrow{ME}$•$\overrightarrow{MF}$=4x₀²-4$\sqrt{3}$x₀，
∵0≤x₀≤$\sqrt{3}$，
∴$\overrightarrow{ME}$•$\overrightarrow{MF}$的最小值为-3，
当点M在边AC上时，
∵直线AC的斜率为$\sqrt{3}$，
∴直线AC的方程为：$\sqrt{3}$x-y+3=0，
设点M（x₀，3+$\sqrt{3}$x₀），则-$\sqrt{3}$≤x₀≤0，
∵$\overrightarrow{ME}$=（-x₀，-$\sqrt{3}$x₀-4），$\overrightarrow{MF}$=（-x₀，-$\sqrt{3}$x₀），
∴$\overrightarrow{ME}$•$\overrightarrow{MF}$=4x₀²+4$\sqrt{3}$x₀，
∵-$\sqrt{3}$≤x₀≤0，
∴$\overrightarrow{ME}$•$\overrightarrow{MF}$的最小值为-3，
综上，$\overrightarrow{ME}$•$\overrightarrow{MF}$的最小值为-3．
故答案为：-3．

点评 本题重点考查了平面向量的基本运算、数量积的运算性质等知识，是综合性题目．