
【题目】已知直线l:y=x+m,m∈R.
(I)若以点M(2,0)为圆心的圆与直线l相切与点P,且点P在y轴上,求该圆的方程;
(II)若直线l关于x轴对称的直线为![]() ,问直线
,问直线![]() 与抛物线C:x2=4y是否相切?说明理由.
与抛物线C:x2=4y是否相切?说明理由.
科目:高中数学 来源: 题型:
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: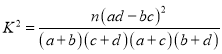 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,其前n项的积为
的各项均为正数,其前n项的积为![]() ,记
,记![]() ,
,![]() .
.
(1)若数列![]() 为等比数列,数列
为等比数列,数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求数列![]() 的通项公式.
的通项公式.
②记![]() ,那么数列
,那么数列![]() 中是否存在两项
中是否存在两项![]() ,(s,t均为正偶数,且
,(s,t均为正偶数,且![]() ),使得数列
),使得数列![]() ,
,![]() ,
,![]() ,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为坐标原点O,对称轴为![]() 轴,其准线为
轴,其准线为![]() .
.
(1)求抛物线C的方程;
(2)设直线![]() ,对任意的
,对任意的![]() 抛物线C上都存在四个点到直线l的距离为
抛物线C上都存在四个点到直线l的距离为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com