
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2 ![]() ,E是PB上任意一点.
,E是PB上任意一点. 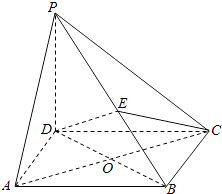
(1)求证:AC⊥DE;
(2)已知二面角A﹣PB﹣D的余弦值为 ![]() ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
【答案】
(1)证明:∵PD⊥平面ABCD,AC平面ABCD
∴PD⊥AC
又∵ABCD是菱形,∴BD⊥AC,BD∩PD=D
∴AC⊥平面PBD,∵DE平面PBD
∴AC⊥DE…(6分)
(2)解:分别以OA,OB,OE方向为x,y,z轴建立空间直角坐标系,设PD=t,则 ![]()
由(1)知:平面PBD的法向量为 ![]() ,
,
令平面PAB的法向量为 ![]() ,则根据
,则根据 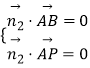 得
得 ![]() ∴
∴ ![]()
因为二面角A﹣PB﹣D的余弦值为 ![]() ,则
,则 ![]() ,即
,即  ,∴
,∴ ![]()
∴ ![]()
设EC与平面PAB所成的角为θ,
∵ ![]() ,
, ![]()
∴ ![]()
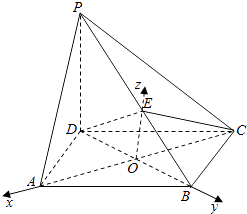
【解析】(1)证明线线垂直,正弦证明线面垂直,即证AC⊥平面PBD;(2)分别以OA,OB,OE方向为x,y,z轴建立空间直角坐标系,设PD=t,用坐标表示点,求得平面PBD的法向量为 ![]() ,平面PAB的法向量为
,平面PAB的法向量为 ![]() ,根据二面角A﹣PB﹣D的余弦值为
,根据二面角A﹣PB﹣D的余弦值为 ![]() ,可求t的值,从而可得P的坐标,再利用向量的夹角公式,即可求得EC与平面PAB所成的角.
,可求t的值,从而可得P的坐标,再利用向量的夹角公式,即可求得EC与平面PAB所成的角.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则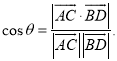 .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,则f(x)是( )
,则f(x)是( )
A.周期为π,图象关于点 ![]() 对称的函数
对称的函数
B.最大值为2,图象关于点 ![]() 对称的函数
对称的函数
C.周期为2π,图象关于点 ![]() 对称的函数
对称的函数
D.最大值为2,图象关于直线 ![]() 对称的函数
对称的函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只小蜜蜂在一个棱长为3的正方体玻璃容器内随机飞行,若蜜蜂在飞行过程中与正方体玻璃容器6个表面中至少有一个的距离不大于1,则就有可能撞到玻璃上面不安全,若始终保持与正方体玻璃容器6个表面的距离均大于1,则飞行是安全的,假设蜜蜂在正方体玻璃容器内飞行到每一位置可能性相同,那么蜜蜂飞行是安全的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1,2,3,4,现从盒子中随机抽取卡片.
(1)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于8的概率;
(2)若随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12:00至13:00间的销售金额,并用茎叶图表示如图.则有( ) 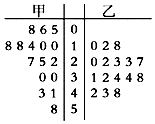
A.甲城销售额多,乙城不够稳定
B.甲城销售额多,乙城稳定
C.乙城销售额多,甲城稳定
D.乙城销售额多,甲城不够稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如下表所示:
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析,发现销售量y对奶茶的价格x具有线性相关关系.
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y= ![]() 中,
中, 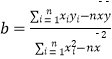 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|+2x(a∈R)
(1)当a=4时,解不等式f(x)≥8;
(2)当a∈[0,4]时,求f(x)在区间[3,4]上的最小值;
(3)若存在a∈[0,4],使得关于x的方程f(x)=tf(a)有3个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷等差数列{an}的前n项和为Sn , 已知a1=1,S3=12.
(1)求a24与S7的值;
(2)已知m、n均为正整数,满足am=Sn . 试求所有n的值构成的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com