
【题目】设a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
【答案】(Ⅰ)f(x)的单调递减区间是(-∞,ln2),单调递增区间是(ln2,+∞),极小值为f(ln2)=eln2-2ln2+2a=2(1-ln2+a);(Ⅱ)求证:当a>ln2-1且x>0时,ex>x2-2ax+1.
【解析】试题分析:(1)由![]() ,知
,知![]() .令
.令![]() ,得
,得![]() .列表讨论能求出
.列表讨论能求出![]() 的单调区间区间及极值.
的单调区间区间及极值.
(2)设![]() ,于是
,于是![]() ,由(1)知当
,由(1)知当![]() 时,
时,![]() 最小值为
最小值为![]() ,于是对任意
,于是对任意![]() ,都有
,都有![]() ,所以
,所以![]() 在
在![]() 内单调递增.由此能够证明
内单调递增.由此能够证明![]() .
.
试题解析:解:∵f(x)=ex﹣2x+2a,x∈R,
∴f′(x)=ex﹣2,x∈R.
令f′(x)=0,得x=ln2.
于是当x变化时,f′(x),f(x)的变化情况如下表:

故f(x)的单调递减区间是(﹣∞,ln2),
单调递增区间是(ln2,+∞),
f(x)在x=ln2处取得极小值,
极小值为f(ln2)=eln2﹣2ln2+2a=2(1﹣ln2+a),无极大值.
(2)证明:设g(x)=ex﹣x2+2ax﹣1,x∈R,
于是g′(x)=ex﹣2x+2a,x∈R.
由(1)知当a>ln2﹣1时,
g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.
于是对任意x∈R,都有g′(x)>0,所以g(x)在R内单调递增.
于是当a>ln2﹣1时,对任意x∈(0,+∞),都有g(x)>g(0).
而g(0)=0,从而对任意x∈(0,+∞),g(x)>0.
即ex﹣x2+2ax﹣1>0,
故ex>x2﹣2ax+1.


科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 ![]() .
. 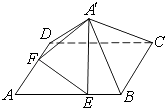
(1)求五棱锥A′﹣BCDFE的体积;
(2)求平面A′EF与平面A′BC的夹角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌汽车4s店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频数 | 40 | 20 | a | 10 | b |
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值.
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率P(A)
(3)求Y的分布列及数学期望EY.
查看答案和解析>>
科目:高中数学 来源: 题型:
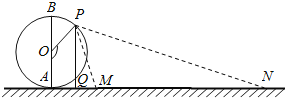
【题目】如图,摩天轮的半径OA为![]() ,它的最低点A距地面的高度忽略不计.地面上有一长度为
,它的最低点A距地面的高度忽略不计.地面上有一长度为![]() 的景观带MN,它与摩天轮在同一竖直平面内,且
的景观带MN,它与摩天轮在同一竖直平面内,且![]() .点P从最低点A处按逆时针方向转动到最高点B处,记
.点P从最低点A处按逆时针方向转动到最高点B处,记![]() .
.
(Ⅰ)当![]() 时,求点P距地面的高度PQ;
时,求点P距地面的高度PQ;
(Ⅱ)设![]() ,写出用
,写出用![]() 表示y的函数关系式,并求y的最大值.
表示y的函数关系式,并求y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x﹣y|=2”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某港湾的平面示意图如图所示, ![]() ,
, ![]() ,
, ![]() 分别是海岸线
分别是海岸线![]() 上的三个集镇,
上的三个集镇, ![]() 位于
位于![]() 的正南方向6km处,
的正南方向6km处, ![]() 位于
位于![]() 的北偏东
的北偏东![]() 方向10km处.
方向10km处.
(Ⅰ)求集镇![]() ,
, ![]() 间的距离;
间的距离;
(Ⅱ)随着经济的发展,为缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 上分别修建码头
上分别修建码头![]() ,开辟水上航线.勘测时发现:以
,开辟水上航线.勘测时发现:以![]() 为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头
为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头![]() 的位置,使得
的位置,使得![]() 之间的直线航线最短.
之间的直线航线最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人投篮命中的概率为别为 ![]() 与
与 ![]() ,各自相互独立,现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立,现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1个的概率;
(2)设ξ表示比赛结束后,甲、乙两人进球数的差的绝对值,求ξ的概率分布和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com