练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知曲线的参数方程为（为参数），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）写出曲线的极坐标方程和直线的直角坐标方程；

    （2）若射线与曲线交于两点，与直线交于点，射线与曲线交于两点，求的面积.

    【答案】（1）；；（2）.

    【解析】

    （1）消掉参数得出曲线的直角坐标方程，再由，得出曲线的极坐标方程和直线的直角坐标方程；

    （2）联立极坐标方程得出的极坐标，进而得出的值，再由直角三角形的边角关系得出点到直线的距离，最后由三角形面积公式计算即可.

    （1）∵，∴，∴，∴

    ∵，∴

    又∵直线的极坐标方程为，∴

    ∴曲线的极坐标方程为，直线的直角坐标方程为

    （2）由题意可知，设点的极坐标为，点的极坐标为，点的极坐标为

    ∴

    ∴

    点到直线的距离为

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象，为了容易看出一个班级的成绩变化，将离散的点用虚线连接，根据图象，给出下列结论：

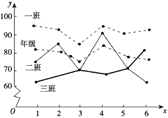
    ①一班成绩始终高于年级平均水平，整体成绩比较好；

    ②二班成绩不够稳定，波动程度较大；

    ③三班成绩虽然多次低于年级平均水平，但在稳步提升.

    其中错误的结论的个数为（ ）

    A.0B.1C.2D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知边长为的等边三角形的一个顶点位于原点，另外两个顶点在抛物线：（）上.

    （1）求抛物线的方程；

    （2）直线交抛物线于，两点，交抛物线的准线于点，交轴于点，若.证明：直线过定点，并求出定点坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年疫情的到来给我们生活学习等各方面带来种种困难.为了顺利迎接高考，省里制定了周密的毕业年级复学计划.为了确保安全开学，全省组织毕业年级学生进行核酸检测的筛查.学生先到医务室进行咽拭子检验，检验呈阳性者需到防疫部门做进一步检测.已知随机抽一人检验呈阳性的概率为0.2%，且每个人检验是否呈阳性相互独立，若该疾病患病率为0.1%，且患病者检验呈阳性的概率为99%.若某人检验呈阳性，则他确实患病的概率（ ）

    A.0.99%B.99%C.49.5%.D.36.5%

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“地摊经济”是李克强总理在本届政府工作报告中向全国人民发出的口号，某生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据，如表所示：

    试销单价（元）

    4

    5

    6

    7

    8

    9

    产品销量（件）

    84

    83

    80

    75

    68

    已知，，，

    （1）试求，若变量，具有线性相关关系，求产品销量（件）关于试销单价（元）的线性回归方程；

    （2）用表示用（1）中所求的线性回归方程得到的与对应的产品销量的估计值．当销售数据对应的残差的绝对值时，则将销售数据称为一个“好数据”．现从6个销售数据中任取2个，求恰好2个都是“好数据”的概率．

    （参考公式：线性回归方程中，的最小二乘估计分别为，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为阻隔新冠肺炎病毒，多地进行封城.封城一段时间后，有的人情绪波动不大，反应一般；也有的人情绪波动大，反应强烈.某社区为了解民众心理反应，随机调查了100位居民，得到数据如下表：

    反应强烈

    反应一般

    合计

    男

    20

    20

    40

    女

    45

    15

    60

    合计

    65

    35

    100

    （1）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若从该社区的男性居民中随机抽取3位，记其中反应强烈的人数为X，求随机变量X的分布列和数学期望；

    （2）根据调查数据，能否在犯错的概率不超过的前提下认为“反应强烈”与性别有关，并说明理由.

    参考数据：

    k

    （参考公式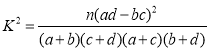：，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，，，、分别为和的中点，且.

    （1）求证：平面；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若且，求的单调区间；

    （2）若在处取得最大值，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在直角坐标系中，曲线由中心在原点，焦点在轴上的半椭圆和以原点为圆心，半径为2的半圆构成，以坐标原点为极点，轴正半轴为极轴建立极坐标系.

    （1）写出曲线的极坐标方程；

    （2）已知射线与曲线交于点，点为曲线上的动点，求面积的最大值.

    查看答案和解析>>

    同步练习册答案