
分析 (Ⅰ)设圆的方程为x2+y2+Dx+Ey+F=0,根据经过P(4,-2),Q(-1,3)两点的圆C半径小于5,且在y轴上截得的线段长为$4\sqrt{3}$,求出D,E,F,即可求圆C的方程;
(Ⅱ)利用直线的平行关系设出直线的方程,利用设而不求的思想得到关于所求直线方程中未知数的方程,通过方程思想确定出所求的方程,注意对所求的结果进行验证和取舍.
解答 解:(Ⅰ) 设圆的方程为x2+y2+Dx+Ey+F=0,
令x=0⇒y2+Ey+F=0,∴y1+y2=-E,y1•y2=F,
∴$4\sqrt{3}=|{y_1}-{y_2}|=\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}•{y_2}}=\sqrt{{E^2}-4F}$,
∴E2-4F=48①…(2分)
又圆过P(4,-2),Q(-1,3)两点,
∴$\left\{{\begin{array}{l}{16+4+4D-2E+F=0}\\{1+9-D+3E+F=0}\end{array}}\right.$$⇒\left\{{\begin{array}{l}{4D-2E+F=-20}\\{-D+3E+F=-10}\end{array}}\right.$⇒2E+F=-12…②
由 ①②得:$\left\{{\begin{array}{l}{D=2}\\{E=0}\\{F=-12}\end{array}}\right.$或$\left\{{\begin{array}{l}{D=-10}\\{E=-8}\\{F=4}\end{array}}\right.$…(4分)
∵圆的半径小于5,∴圆的方程为x2+y2-2x-12=0…(6分)
(Ⅱ)${k_{PQ}}=\frac{3-(-2)}{-1-4}=-1$,∴设l的方程为:x+y+m=0…(7分)
由$\left\{{\begin{array}{l}{x+y+m=0}\\{{x^2}+{y^2}-2x-12=0}\end{array}}\right.$⇒2x2+(2m-2)x+m2-12=0,
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=1-m,{x_1}•{x_2}=\frac{{{m^2}-12}}{2}$…(9分)
∵以AB为直径的圆过原点,∴OA⊥OB,…(10分)
∴x1•x2+y1•y2=x1•x2+(-x1-m)•(-x2-m)=0
整理得:m2+m-12=0⇒m=3或m=-4,…(11分)
且m=3或m=-4均满足△>0…(12分)
∴l的方程为x+y+3=0或x+y-4=0…(13分)
点评 本题考查直线与圆的综合问题,考查直线方程的求解方法和圆方程的求解方法,注意待定系数法的运用,考查学生对直线与圆相交弦长有关问题的处理方法,考查设而不求思想的运用,考查方程思想和转化与化归的思想,是中档题.


科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:解答题
给定函数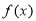 ,若对于定义域中的任意
,若对于定义域中的任意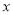 ,都有
,都有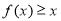 恒成立,则称函数
恒成立,则称函数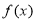 为“爬坡函数”.
为“爬坡函数”.
(1)证明:函数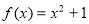 是爬坡函数;
是爬坡函数;
(2)若函数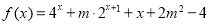 是爬坡函数,求实数m的取值范围;
是爬坡函数,求实数m的取值范围;
(3)若对任意的实数b,函数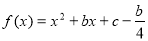 都不是爬坡函数,求实数c的取值范围.
都不是爬坡函数,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com