【题目】下列说法错误的是（ ）（多选）
A.有一个面是多边形，其余各面都是三角形，由这些面围成的多面体是棱锥
B.有两个面平行且相似，其余各面都是梯形的多面体是棱台
C.如果一个棱锥的各个侧面都是等边三角形，那么这个棱锥可能为六棱锥
D.如果一个棱柱的所有面都是长方形，那么这个棱柱是长方体
【答案】ABC
【解析】
选项
不符合棱锥，棱台定义，所以错误；选项
，会得出棱锥的各个侧面的共顶点的角之和是
，构成平面图形，所以错误；选项
，可推出侧棱与底面垂直，所以正确.
选项A，有一个面是多边形，其余各面都是有一个公共顶点的三角形，
由这些面所围成的多面体叫做棱锥，即其余各面的三角形必须有公共的顶点，
故A错误；
选项B，棱台是由棱锥被平行于棱锥底面的平面所截而得的，
而有两个面平行且相似，其余各面都是梯形的多面体有可能不是棱台，
因为它的侧棱延长后不一定交于一点，故B错误；
选项C，当棱锥的各个侧面的共顶点的角之和是时，
各侧面构成平面图形，故这个棱锥不可能为六棱锥，故C错误；
选项D，若每个侧面都是长方形则说明侧棱与底面垂直，
又底面也是长方形，符合长方体的定义，故D正确.
故选:ABC.
每课必练系列答案
巧学巧练系列答案科目：高中数学 来源： 题型：
【题目】对于函数
，定义f1（x）=f（x），fn+1（x）=f[fn（x）]（n∈N*），已知偶函数g（x）的定义域为（﹣∞，0）∪（0，+∞），g（1）=0，当x＞0且x≠1时，g（x）=f2018（x）．
（1）求f2（x），f3（x），f4（x），f2018（x）；
（2）求出函数y=g（x）的解析式；
（3）若存在实数a、b（a＜b），使得函数g（x）在[a，b]上的值域为[mb，ma]，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，离心率
，且椭圆的短轴长为2.
（1）球椭圆的标准方程；
（2）已知直线
过右焦点
，且它们的斜率乘积为
，设分别与椭圆交于点
和
.
①求
的值；
②设
的中点
，
的中点为，求
面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，
，过点
的直线与椭圆
交于
两点，延长
交椭圆于点
，
的周长为8.
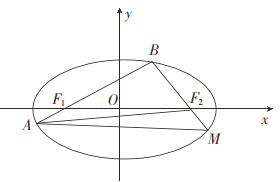
（1）求的离心率及方程；
（2）试问：是否存在定点
，使得
为定值？若存在，求
；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4－4：坐标系与参数方程]
在直角坐标系
中，曲线
的参数方程为
（
为参数），直线
的参数方程为
（
为参数）.
（1）求和的直角坐标方程；
（2）若曲线截直线所得线段的中点坐标为
，求的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A. 某厂一批产品的次品率为
，则任意抽取其中10件产品一定会发现一件次品
B. 掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0.5
C. 某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈
D. 气象部门预报明天下雨的概率是90%，说明明天该地区90%的地方要下雨，其余10%的地方不会下雨
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线C1的渐近线是
x±2y=0，焦点坐标是F1（-
，0）、F2（，0）．
（1）求双曲线C1的方程；
（2）若椭圆C2与双曲线C1有公共的焦点，且它们的离心率之和为
，点P在椭圆C2上，且|PF1|=4，求∠F1PF2的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
