
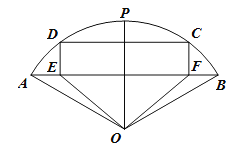
【题目】有一块圆心角为120度,半径为![]() 的扇形钢板
的扇形钢板![]() (
(![]() 为弧
为弧![]() 的中点),现要将其裁剪成一个五边形磨具
的中点),现要将其裁剪成一个五边形磨具![]() ,其下部为等腰三角形
,其下部为等腰三角形![]() ,上部为矩形
,上部为矩形![]() .设
.设![]() 五边形
五边形![]() 的面积为
的面积为![]() .
.
(1)写出![]() 关于
关于![]() 的函数表达式,并写出
的函数表达式,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
【答案】(1) S=![]() R2sinα(4cosα-1)(0<α<
R2sinα(4cosα-1)(0<α<![]() )(2)
)(2) ![]()
【解析】
(1)根据直角三角形解得矩形![]() 的长与宽以及等腰三角形
的长与宽以及等腰三角形![]() 的底与高,再根据矩形面积公式以及三角形面积公式求结果,最后根据实际意义确定
的底与高,再根据矩形面积公式以及三角形面积公式求结果,最后根据实际意义确定![]() 的取值范围;(2)利用导数求函数最值.
的取值范围;(2)利用导数求函数最值.
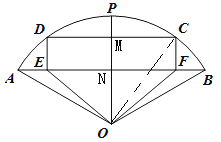
(1)如图,设OP与CD、AB交于M,N两点,
![]() 为弧
为弧![]() 的中点,则M为CD中点,OP⊥AB,
的中点,则M为CD中点,OP⊥AB,
OM=OCcosα=Rcosα,CM=OCsinα=Rsinα,则EF=CD=2CM=2Rsinα
∠POB=![]() ∠AOB=60°,∠OBN=30°,
∠AOB=60°,∠OBN=30°,
所以,ON=![]() OB=
OB=![]() R,
R,
CF=MN=OM-ON=Rcosα-![]() R
R
所以,S=CDCF+![]() EFON=2Rsinα×(Rcosα-
EFON=2Rsinα×(Rcosα-![]() R)+
R)+![]() ×2Rsinα×
×2Rsinα×![]() R
R
=![]() R2sinα(4cosα-1)(0<α<
R2sinα(4cosα-1)(0<α<![]() )
)
(2)设f(α)=sinα(4cosα-1),则
![]() =
=![]() =0
=0
因为0<α<![]() ,所以,
,所以,![]()

由表可,当S取得最大值时,![]()


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 将几何体
将几何体![]() 分成上下两部分的体积比为
分成上下两部分的体积比为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距离车站10km处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在距离车站( )
A.4kmB.5kmC.6kmD.7km
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2018年10月1日起,![]() 中华人民共和国个人所得税
中华人民共和国个人所得税![]() 新规定,公民月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
新规定,公民月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3 |
超过1500元不超过4500元的部分 | 10 |
超过4500元不超过9000元的部分 | 20 |
超过9000元不超过35000元 | 25 |
|
|
![]() 如果小李10月份全月的工资、薪金为7000元,那么他应该纳税多少元?
如果小李10月份全月的工资、薪金为7000元,那么他应该纳税多少元?
![]() 如果小张10月份交纳税金425元,那么他10月份的工资、薪金是多少元?
如果小张10月份交纳税金425元,那么他10月份的工资、薪金是多少元?
![]() 写出工资、薪金收入
写出工资、薪金收入![]() 元
元![]() 月
月![]() 与应缴纳税金
与应缴纳税金![]() 元
元![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对称轴为坐标轴的椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且直线
两点,且直线![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,则当
的斜率依次成等比数列,则当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() .沿
.沿![]() 将△
将△![]() 翻折到△
翻折到△![]() ,连接
,连接![]() ,得到如图的五棱锥
,得到如图的五棱锥![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“生成数列”.
的“生成数列”.
(1)若数列![]() 的“生成数列”是
的“生成数列”是![]() ,求
,求![]() ;
;
(2)若![]() 为偶数,且
为偶数,且![]() 的“生成数列”是
的“生成数列”是![]() ,证明:
,证明:![]() 的“生成数列”是
的“生成数列”是![]() ;
;
(3)若![]() 为奇数,且
为奇数,且![]() 的“生成数列”是
的“生成数列”是![]() ,
,![]() 的“生成数列”是
的“生成数列”是![]() ,…,依次将数列
,…,依次将数列![]() ,
,![]() ,
,![]() ,…的第
,…的第![]() 项取出,构成数列
项取出,构成数列![]() .
.
探究:数列![]() 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com