
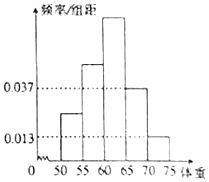
 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.分析 (I)由频率分布直方图先求出前3个小组的频率,从而得到第2小组的频率,由此能求出高三毕业班想参军的学生人数.
(II)根据X服从二项分布,$P(X=k)=C_2^k{(\frac{5}{8})^k}{(\frac{3}{8})^{3-k}}$,K=0,1,2,3求解分布列,数学期望.
解答 解:(Ⅰ)由频率分布直方图知:
前3个小组的频率为:1-(0.013+0.037)×5=0.75,
所以第1小组的频率为$\frac{1}{6}$×0.75=0.125,
第2小组的频率为$\frac{2}{6}$×0.75=0.25,
第3小组的频率为$\frac{3}{6}$×0.75=0.5,
所以该校高三毕业班想参军的学生人数是24÷0.25=96.
(Ⅱ)分布列见解析,$\frac{15}{8}$.
(Ⅱ)由(1)可得,一个想参军的学生体重超过60公斤的概率为$p={p_3}+(0.037+0.013)×5=\frac{5}{8}$.
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{512}$ | $\frac{45}{512}$ | $\frac{75}{512}$ | $\frac{125}{512}$ |
点评 本题考查该校高三毕业班想参军的学生人数的求法,解题时要注意频率分布直方图的合理运用,难度不大,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
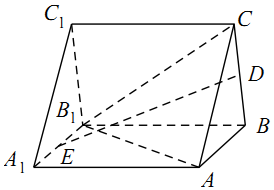 在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com