
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)单调增区间为(﹣∞,0),单调减区间为(0,+∞).(2)![]()
【解析】试题分析:(1)先求出![]() 的定义域,再利用导数判断
的定义域,再利用导数判断![]() 的单调性,
的单调性,
(2)分类参数可得![]() ,利用导数求出
,利用导数求出![]() 的最值或极限即可得出
的最值或极限即可得出![]() 的范围.
的范围.
试题解析:(1)令g(x)=xex,则g′(x)=ex(1+x),
∴当x<﹣1时,g′(x)<0,当x>﹣1时,g′(x)>0,
∴g(x)≥g(﹣1)=﹣![]() ,即xex≥﹣
,即xex≥﹣![]() >﹣1,
>﹣1,
∴xex+1>0恒成立,
∴f(x)的定义域为R.
f′(x)=![]() =
=![]() ,
,
令f′(x)>0得x<0,令f′(x)<0得x>0,
∴f(x)的单调增区间为(﹣∞,0),单调减区间为(0,+∞).
(2)当x>0时,f(x)>0,ax2+1>0(a≥0),
∵![]() ,
,
∴a>![]() ﹣
﹣![]() +
+![]() (x>0),
(x>0),
令h(x)=![]() ﹣
﹣![]() +
+![]() (x>0),
(x>0),
则h′(x)=﹣![]() +
+![]() ﹣
﹣![]() =
=![]() ,
,
令p(x)=2ex﹣2﹣x﹣xex(x>0),则p′(x)=ex﹣1﹣xex,
∴p″(x)=﹣xex<0,
∴P′(x)在(0,+∞)上单调递减,∴p′(x)<p′(0)=0,
∴p(x)在(0,+∞)上单调递减,∴p(x)<p(0)=0,
∴h′(x)<0,
∴h(x)在(0,+∞)上单调递减,
又h(x)=![]() ,
,
∴![]() =
=![]()
![]() =
=![]() ,
,
∴h(x)<![]() ,
,
∴a≥![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.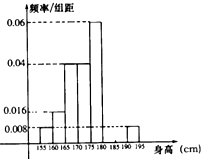
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x﹣y|≤5的事件概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R). 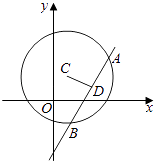
(1)求证:无论m取什么实数,直线l恒过第一象限;
(2)求直线l被圆C截得的弦长最短时m的值以及最短长度;
(3)设直线l与圆C相交于A、B两点,求AB中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且对任意x1 , x2∈(0,+∞)都有 ![]() <0(x1≠x2),若实数a满足f(log3a﹣1)+2f(
<0(x1≠x2),若实数a满足f(log3a﹣1)+2f( ![]() a)≥3f(1),则a的取值范围是( )
a)≥3f(1),则a的取值范围是( )
A.[ ![]() ,3]
,3]
B.[1,3]
C.(0, ![]() )
)
D.(0,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域R上的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣4f(x),求g(x)在[1,+∞)上的最小值.
,且g(x)=a2x+a﹣2x﹣4f(x),求g(x)在[1,+∞)上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com