
【题目】某地区业余足球运动员共有15000人,其中男运动员9000人,女运动员6000人,为调查该地区业余足球运动员每周平均踢足球占用时间的情况,采用分层抽样的方法,收集300位业务足球运动员每周平均踢足球占用时间的样本数据(单位:小时)
得到业余足球运动员每周平均踢足球所占用时间的频率分布直方图(如图所示),其中样本数据分组区间为:(0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
将“业务运动员的每周平均踢足球时间所占用时间超过4小时”
定义为“热爱足球”.
附:K2= ![]()
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
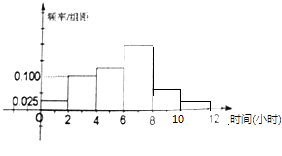
(1)应收集多少位女运动员样本数据?
(2)估计该地区每周平均踢足球所占用时间超过4个小时的概率.
(3)在样本数据中,有80位女运动员“热爱足球”.请画出“热爱足球与性别”列联表,并判断是否有99%的把握认为“热爱足球与性别有关”.
【答案】
(1)解: ![]() ,
,
∴应收集120位女运动员样本数据
(2)解:由频率分布直方图得1﹣2×(0.100+0.025)=0.75,
∴该地区每周平均踢足球所占用时间超过4个小时的概率的估计值为0.75
(3)解:由(2)知,300位足球运动中有300×0.75=225人的每周平均踢足球时间超过4小时,
75人的每周平均踢足球占用时间超过4小时,
∴热爱足球与性别列联表如下,
男运动员 | 女运动员 | 总计 | |
不热爱足球 | 35 | 40 | 75 |
热爱足球 | 145 | 80 | 225 |
总计 | 180 | 120 | 300 |
结合列联表可算得 ![]() =
= ![]() .
.
∴有99%的把握认为“热爱足球与性别有关”
【解析】(1)利用分层抽样中每层所抽取的比例数相等求得答案;(2)由频率分布直方图结合概率和为1求得该地区每周平均踢足球所占用时间超过4个小时的概率.(3)由题意列出2×2列联表,计算出k2的值,结合附表得答案.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在半径为R的圆桌上摆放同样大小的半径为r的硬币.要求硬币不准露出圆桌面边缘,并且所摆硬币彼此不能重叠.当摆放n枚硬币之后,圆桌上就不能再多摆放一枚这种硬币了.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过圆O外一点P作圆的切线PC,切点为C,割线PAB、割线PEF分别交圆O于A与B、E与F.已知PB的垂直平分线DE与圆O相切. 
(1)求证:DE∥BF;
(2)若 ![]() ,DE=1,求PB的长.
,DE=1,求PB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双曲线的方程为![]() ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】双曲线的方程为![]() ,则渐近线方程为
,则渐近线方程为![]() ,渐近线方程为:
,渐近线方程为: ![]() ,反之当渐近线方程为
,反之当渐近线方程为![]() 时,只需要满足
时,只需要满足![]() ,等轴双曲线即可.故选择充分不必要条件.
,等轴双曲线即可.故选择充分不必要条件.
故答案为:A.
【题型】单选题
【结束】
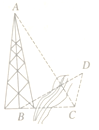
10
【题目】如图,为测量河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,在点
的正东方向上,在点![]() 处测得
处测得![]() 点的仰角为
点的仰角为![]() ,再由点
,再由点![]() 沿北偏东
沿北偏东![]() 方向走
方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是( )
的高是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边分别为a,b,c,且c<a,已知 ![]() =﹣2,tanB=2
=﹣2,tanB=2 ![]() ,b=3.
,b=3.
(1)求a和c的值;
(2)求sin(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)根据二倍角公式和两角和差公式得到![]() ,进而得到周期;(2)由
,进而得到周期;(2)由![]() ,得到
,得到![]() ,
, ![]() ,由配凑角公式得到
,由配凑角公式得到![]() ,代入值得到函数值.
,代入值得到函数值.
解析:
(1)由题意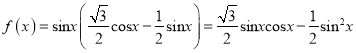
![]() =
=![]()
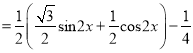
![]()
所以![]() 的最小正周期为
的最小正周期为![]() ;
;
(2)由![]()
![]()
又由![]() 得
得![]() ,所以
,所以![]()
故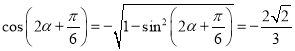 ,
,
故![]()
![]()
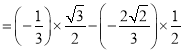
![]()
【题型】解答题
【结束】
20
【题目】为响应十九大报告提出的实施乡村振兴战略,某村庄投资![]() 万元建起了一座绿色农产品加工厂.经营中,第一年支出
万元建起了一座绿色农产品加工厂.经营中,第一年支出![]() 万元,以后每年的支出比上一年增加了
万元,以后每年的支出比上一年增加了![]() 万元,从第一年起每年农场品销售收入为
万元,从第一年起每年农场品销售收入为![]() 万元(前
万元(前![]() 年的纯利润综合=前
年的纯利润综合=前![]() 年的 总收入-前
年的 总收入-前![]() 年的总支出-投资额
年的总支出-投资额![]() 万元).
万元).
(1)该厂从第几年开始盈利?
(2)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() .
.
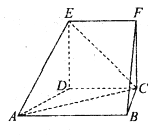
(1)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 或其延长线上是否存在点
或其延长线上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线相交于
与抛物线相交于![]() 两点,分别过点
两点,分别过点![]() 作抛物线的两条切线
作抛物线的两条切线![]() 和
和![]() ,记
,记![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)证明:直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)求证:点![]() 在一条定直线上.
在一条定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com